题目内容
11.为了迎接“五•一”小长假的购物高峰.某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表:| 运动鞋价格 | 甲 | 乙 |
| 进价(元/双) | m | m-20 |
| 售价(元/双) | 240 | 160 |
(1)求m的值;
(2)要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价-进价)不少于21700元,且不超过22300元,问该专卖店有几种进货方案?该专卖店要获得最大利润应如何进货?
分析 (1)用总价除以单价表示出购进鞋的数量,根据两种鞋的数量相等列出方程求解即可;
(2)设购进甲种运动鞋x双,表示出乙种运动鞋(200-x)双,然后根据总利润列出一元一次不等式,求出不等式组的解集后,再根据鞋的双数是正整数解答;设总利润为W,表示出利润,求得最值即可.
解答 解:(1)依题意得,
$\frac{3000}{m}$=$\frac{2400}{m-20}$,
整理得,3000(m-20)=2400m,
解得:m=100,
经检验,m=100是原分式方程的解,
所以,m=100;
(2)设购进甲种运动鞋x双,则乙种运动鞋(200-x)双,
根据题意得,
$\left\{\begin{array}{l}{(240-100)x+(160-80)(200-x)≥21700}\\{(240-100)x+(160-80)(200-x)≤22300}\end{array}\right.$
不等式组的解集是95≤x≤105,
∵x是正整数,105-95+1=11,
∴共有11种方案.
设总利润为W,则W=(240-100)x+80(200-x)=60x+16000(95≤x≤105),
所以,当x=105时,W有最大值,
即此时应购进甲种运动鞋105双,购进乙种运动鞋95双.
点评 本题考查了分式方程的应用,一元一次不等式组的应用,解决问题的关键是读懂题意,找到关键描述语,进而找到所求的量的等量关系和不等关系,解决问题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
2.某校为纪念世界反法西斯战争70周年,举行了主题为“让历史照亮未来”的演讲比赛,其中九年级的5位参赛选手的比赛成绩(单位:分)分别为:8.6,9.5,9.7,8.8,9,则这5个数据的中位数是( )
| A. | 9.7 | B. | 9.5 | C. | 9 | D. | 8.8 |
20.已知O为△ABC的内心,∠A=68°,则∠BOC的度数是( )
| A. | 136° | B. | 34° | C. | 168° | D. | 124° |
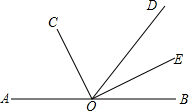 如图所示,已知点A、O、B在同一条直线上,且OC、OE分别是∠AOD、∠BOD的角平分线,若∠BOD=72°,求∠COD和∠COE的度数.
如图所示,已知点A、O、B在同一条直线上,且OC、OE分别是∠AOD、∠BOD的角平分线,若∠BOD=72°,求∠COD和∠COE的度数.