题目内容
6.甲安装队在A小区安装66台空调,乙安装队为B小区安装60台空调,两队同时开工且恰好同时完工,甲队比乙队每天多安装2台.问甲、乙安装队每天安装几台空调?分析 求的是工效,工作总量明显,一定是根据工作时间来列等量关系,本题的关键描述语是:两队同时开工且恰好同时完工.等量关系为:甲安66台的时间=乙安60台用的时间.
解答 解:设乙队每天安装x台空调,则甲队每天安装(x+2)台空调,
根据题意得,
$\frac{66}{x+2}$=$\frac{60}{x}$
解得x=20,
经检验,x=20是原方程的根,
甲队每天安装x+2=20+2=22(台)
答:甲队每天安装22台空调,乙队每天安装20台空调.
点评 此题考查分式方程的应用,分析题意,找到关键描述语,找到合适的等量关系是解决问题的关键.此题涉及的数量关系:工作总量=工作效率×工作时间.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
14.计算(-ax-1)4结果是( )
| A. | a4x-1 | B. | -a4x-4 | C. | a4x-4 | D. | -a4x-1 |
11.为了迎接“五•一”小长假的购物高峰.某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表:
已知:用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量相同.
(1)求m的值;
(2)要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价-进价)不少于21700元,且不超过22300元,问该专卖店有几种进货方案?该专卖店要获得最大利润应如何进货?
| 运动鞋价格 | 甲 | 乙 |
| 进价(元/双) | m | m-20 |
| 售价(元/双) | 240 | 160 |
(1)求m的值;
(2)要使购进的甲、乙两种运动鞋共200双的总利润(利润=售价-进价)不少于21700元,且不超过22300元,问该专卖店有几种进货方案?该专卖店要获得最大利润应如何进货?
18.下列各度数不是多边形的内角和的是( )
| A. | 1800° | B. | 540° | C. | 1700° | D. | 1080° |
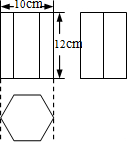 如图是一个上下底密封纸盒的三视图,请你根据图中数据,计算这个密封纸盒的表面积为360+75$\sqrt{3}$cm2.(结果可保留根号).
如图是一个上下底密封纸盒的三视图,请你根据图中数据,计算这个密封纸盒的表面积为360+75$\sqrt{3}$cm2.(结果可保留根号).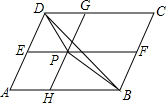 如图,点P为平行四边形ABCD内一点,过P点分别作AB、AD的平行线,交平行四边形ABCD的各边于点E、F、G、H.已知四边形AHPE的面积为3,四边形PFCG的面积为5,则△BDP的面积是1.
如图,点P为平行四边形ABCD内一点,过P点分别作AB、AD的平行线,交平行四边形ABCD的各边于点E、F、G、H.已知四边形AHPE的面积为3,四边形PFCG的面积为5,则△BDP的面积是1.