题目内容
6.已知点A(-1,0)、B(3,0)、C(2,3),D(0,5).(1)求四边形ABCD的面积;
(2)若点E从A点出发向B点运动,运动速度为每秒1个单位长度,设运动时间为ts,是否存在实数t使得线段CE把四边形ABCD的面积分成相等的两部分?若存在,求出t的值及点E的坐标;若不存在,请说明理由.
分析 (1)过C作CM⊥x轴于M,根据图形的面积的和差即可得到结论;
(2)根据题意得到BE=4-t,根据三角形的面积公式列方程即可得到结论.
解答  解:(1)过C作CM⊥x轴于M,则M(2,0),
解:(1)过C作CM⊥x轴于M,则M(2,0),
则四边形ABCD的面积=△DAO的面积+△BCM的面积+梯形CDAM的面积=$\frac{1}{2}$×1×5+$\frac{1}{2}$×1×3+$\frac{1}{2}$×2×(3+5)=12;
(2)假设存在,∵点E从A点出发向B点运动,运动速度为每秒1个单位长度,
∴AE=t,
则BE=5-t,由题意得△BCE的面积=$\frac{1}{2}$×2(4-t)=$\frac{1}{2}$×12,解得:t=-2,
∵0≤t≤4,
∴不存在实数t使得线段CE把四边形ABCD的面积分成相等的两部分.
点评 本题综合考查了梯形的三角形的面积,以及点的坐标,理清点P的运动过程以及相关的线段的长度的表示是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.已知反比例函数y=$\frac{m-3}{x}$的图象经过第一、三象限,则符合条件的m是( )
| A. | m=-1 | B. | m=0 | C. | m=3 | D. | m=5 |
15.下列函数中,经过一、二、四象限的函数是( )
| A. | y=7 | B. | y=-2x | C. | y=-2x-7 | D. | y=-2x+7 |
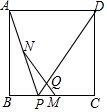 已知:正方形ABCD中,M、N分别是BC、AP的中点,问△PQM的形状并说明理由.
已知:正方形ABCD中,M、N分别是BC、AP的中点,问△PQM的形状并说明理由. 如图,图中所有的三角形都是直角三角形,四边形都是正方形,已知正方形A,B,C,D的边长分别是12,16,9,12,则最大正方形E的面积是625.
如图,图中所有的三角形都是直角三角形,四边形都是正方形,已知正方形A,B,C,D的边长分别是12,16,9,12,则最大正方形E的面积是625.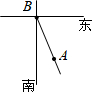 如图,如果张江高科技园区(A)位于复旦大学(B)的南偏东30°的方向,那么复旦大学(B)位于张江高科技园区(A)的北偏西30°或西偏北60°方向.
如图,如果张江高科技园区(A)位于复旦大学(B)的南偏东30°的方向,那么复旦大学(B)位于张江高科技园区(A)的北偏西30°或西偏北60°方向.