题目内容

1．如图，图中所有的三角形都是直角三角形，四边形都是正方形，已知正方形A，B，C，D的边长分别是12，16，9，12，则最大正方形E的面积是625．

分析 根据勾股定理的几何意义解答即可．

解答 解：根据勾股定理的几何意义，可知
SE=SF+SG
=SA+SB+SC+SD
=122+162+92+122
=625；
故答案为：625．

点评 本题考查了勾股定理，熟悉勾股定理的几何意义是解题的关键．

练习册系列答案
相关题目
11．某市一种出租车的起步价为10元，两位乘客分别乘这种出租车走了10km和14km，车费分别为21.2元和27.6元，假设一路顺利，没有停车等候，且不考虑计程器计费的某些特殊规定．请你算出这种出租车起步价所允许行驶的最远路程；并算出超过起步路程但行驶不到15km时，超过部分每千米车费为多少元？
12．对于实数a，b，c，d，规定一种运算$|\begin{array}{l}{a}&{b}\\{c}&{d}\end{array}|$=ad-bc，如$|\begin{array}{l}{1}&{0}\\{2}&{（-2）}\end{array}|$=1×（-2）-0×2=-2，那么当$|\begin{array}{l}{2x}&{x}\\{-x}&{x}\end{array}|$=6时，x的值为（　　）
A．$\sqrt{6}$B．±$\sqrt{6}$C．$\sqrt{2}$D．±$\sqrt{2}$
9．先说出下列各式中的被开方数，再判断各式的结果正确与否，并把不正确的改正过来．
（1）$\sqrt{{3}^{2}}=3$；                        （2）-$\sqrt{{3}^{2}}$=3；
（3）$\sqrt{（-3）^{2}}=-3$；                 （4）±$\sqrt{（-3）^{2}}$=±3．
16．下列各组数中，全部都是有理数的是（　　）
A．-2，0，3，$\sqrt{3}$B．$\frac{1}{7}$，$\frac{1}{3}$，πC．$\sqrt{3}$，π，0D．-2，$\frac{1}{7}$，0
6．已知点A（-1，0）、B（3，0）、C（2，3），D（0，5）．
（1）求四边形ABCD的面积；
（2）若点E从A点出发向B点运动，运动速度为每秒1个单位长度，设运动时间为ts，是否存在实数t使得线段CE把四边形ABCD的面积分成相等的两部分？若存在，求出t的值及点E的坐标；若不存在，请说明理由．
13．一次函数y=kx+b的图象如图所示，则不等式kx+b＞0的解集是x＜3．
10．小华将直角坐标系中的猫的图案向右平移了3个单位长度，平移前猫左眼的坐标为（-4，3）、则移动后猫左眼的坐标为（-1，3）．
11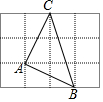．如图，将△ABC放在正方形网格中（图中每个小正方形边长均为1）点A，B，C恰好在网格图中的格点上，那么∠ABC的度数为（　　）
A．90°B．60°C．30°D．45°

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网