题目内容
1.某商店销售一批服装,每件赢利10元时,平均每天可售出800件,经市场调查发现:(1)若为了尽快减少库存,商店采取降低价格策略,则每件衬衫每降价1元,平均每天可多售出300件;
(2)若要提升价格,每件衬衫每涨价5元,平均每天销售量将减少100件,根据总部要求商店平均每天要赢利12000元,该商店可以采取哪些措施达到目的?
分析 (1)设每件降低x元.根据利润=每件的利润×销售数量,列出方程即可解决问题.
(2)每件衬衫涨y元.根据利润=每件的利润×销售数量,列出方程即可解决问题.
解答 解:(1)设每件降低x元.
由题意(10-x)(800+300x)=12000,
解得x=4或$\frac{10}{3}$.
∴总部要求商店平均每天要赢利12000元,可以采取每件降低4元或$\frac{10}{3}$元.
(2)每件衬衫涨y元.
由题意(10+y)(800-20y)=12000,
解得t=10或20,
∴总部要求商店平均每天要赢利12000元,可以采取每件衬衫涨10元或20元.
点评 此题主要考查了一元二次方程的应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解.

练习册系列答案
相关题目
10.数据4,x,0,1,3的平均数是2,则这组数据的方差是( )
| A. | 2 | B. | $\sqrt{2}$ | C. | 3 | D. | 4 |
11. 如图,在菱形ABCD中,对角线AC与BD相交于点O,且AC=6,BD=8,则菱形ABCD的高AH的值是( )
如图,在菱形ABCD中,对角线AC与BD相交于点O,且AC=6,BD=8,则菱形ABCD的高AH的值是( )
 如图,在菱形ABCD中,对角线AC与BD相交于点O,且AC=6,BD=8,则菱形ABCD的高AH的值是( )
如图,在菱形ABCD中,对角线AC与BD相交于点O,且AC=6,BD=8,则菱形ABCD的高AH的值是( )| A. | 4 | B. | 5 | C. | $\frac{24}{5}$ | D. | $\frac{48}{5}$ |
 如图所示.(V球=$\frac{4}{3}$πr3)
如图所示.(V球=$\frac{4}{3}$πr3)
 如图,在Rt△AOB中,OA=OB=3$\sqrt{2}$,⊙O的半径为$\sqrt{2}$,点P是AB边上的一动点,过点P作⊙O的一条切线PQ(点Q为切点),则PQ长度的取值范围为$\sqrt{7}$≤PQ≤4.
如图,在Rt△AOB中,OA=OB=3$\sqrt{2}$,⊙O的半径为$\sqrt{2}$,点P是AB边上的一动点,过点P作⊙O的一条切线PQ(点Q为切点),则PQ长度的取值范围为$\sqrt{7}$≤PQ≤4.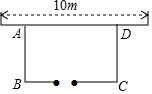 如图,用一段长为15m的篱笆围成一个一边靠墙的矩形菜园,墙长为10m,其中一边BC留一道1m宽的门.
如图,用一段长为15m的篱笆围成一个一边靠墙的矩形菜园,墙长为10m,其中一边BC留一道1m宽的门.