题目内容
12．若|m-4|与n2-8n+16互为相反数，把多项式a2+4b2-mab-n因式分解．分析 根据|m-4|与n2-8n+16互为相反数，得到|m-4|+n2-8n+16=0，求得m=4，n=4，代入代数式进行分解因式即刻得到结论．
解答 解：∵|m-4|与n2-8n+16互为相反数，
∴|m-4|+n2-8n+16=0，
∴|m-4|+（n-4）2=0，
∴m-4=0，n-4=0，
∴m=4，n=4，
∴a2+4b2-mab-n=a2+4b2-4ab-4=（a2+4b2-4ab）-4=（a-2b）2-22=（a-2b+2）（a-2b-2）．
点评 此题主要考查了非负数的性质，分组分解法-分解因式，熟练应用完全平方公式是解题关键．
练习册系列答案
相关题目
3．（a-1）（a+1）（a2+1）-（a4+1）的值是（ ）
| A． | -2a2 | B． | 0 | C． | -2 | D． | -1 |
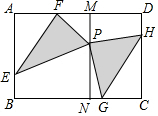如图，在矩形ABCD中，AD=6，AB=4，点E、G、H、F分别在AB、BC、CD、AD上，且AF=CG=2，BE=DH=1，点M在线段DF上，点N在线段BG上，MN∥AB，点P线段MN上，连接PE、PF、PG、PH，则△PEF和△PGH的面积和等于7．
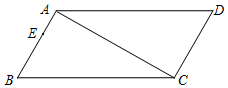如图，在四边形ABCD中，∠B=∠D=60°，∠BAC=∠ACD=90°，点E为边AB上一点，AB=3AE=3cm，动点P从B点出发，以1cm/s的速度沿BC→CD→DA运动至A点停止，设运动时间为t秒．
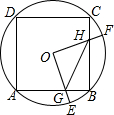如图，边长为4的正方形ABCD内接于⊙O，点E是AB上的一动点（不与A，B重合），点F是BC上的一点，连接OE，OF，分别与AB，BC交于点G，H，且∠EOF=90°．