题目内容
11. 如图,在菱形ABCD中,对角线AC与BD相交于点O,且AC=6,BD=8,则菱形ABCD的高AH的值是( )
如图,在菱形ABCD中,对角线AC与BD相交于点O,且AC=6,BD=8,则菱形ABCD的高AH的值是( )| A. | 4 | B. | 5 | C. | $\frac{24}{5}$ | D. | $\frac{48}{5}$ |
分析 根据菱形的对角线互相垂直平分可得AC⊥BD,再求出OB、OC,然后利用勾股定理列式求出BC,然后根据菱形的面积等于对角线乘积的一半和底边乘以高两种方法列方程求解即可.
解答 解:∵菱形ABCD,
∴AC⊥BD,
OB=$\frac{1}{2}$BD=$\frac{1}{2}$×8=4,
OC=$\frac{1}{2}$AC=$\frac{1}{2}$×6=3,
由勾股定理得,BC=$\sqrt{O{B}^{2}+O{C}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5,
S菱形ABCD=$\frac{1}{2}$AC•BD=BC•AH,
即$\frac{1}{2}$×6×8=5AH,
解得AH=$\frac{24}{5}$.
故选C.
点评 本题考查了菱形的性质,勾股定理,主要利用了菱形的对角线互相垂直平分以及菱形的面积的两种求法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
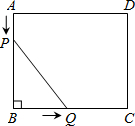 在矩形ABCD中,已知AB=5cm,BC=6cm,点P从点A开始沿边AB向终点B以1cm/s的速度运动;同时,点Q从点B开始沿边BC向终点C以2cm/s的速度运动.当点Q运动到点C时,两点停止运动.设运动时间为t秒.
在矩形ABCD中,已知AB=5cm,BC=6cm,点P从点A开始沿边AB向终点B以1cm/s的速度运动;同时,点Q从点B开始沿边BC向终点C以2cm/s的速度运动.当点Q运动到点C时,两点停止运动.设运动时间为t秒.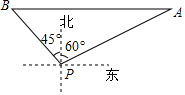 如图,一艘轮船位于灯塔P北偏东60°方向上,距离灯塔40海里的A处,它向西航行多少海里到达灯塔P北偏西45°方向上的B处.(参考数据:$\sqrt{3}$≈1.732,结果精确到0.1)
如图,一艘轮船位于灯塔P北偏东60°方向上,距离灯塔40海里的A处,它向西航行多少海里到达灯塔P北偏西45°方向上的B处.(参考数据:$\sqrt{3}$≈1.732,结果精确到0.1)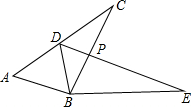 如图,已知△ABC≌△DBE,点D在AC上,BC与DE交于点P,若AD=DC=2.4,BC=4.1.
如图,已知△ABC≌△DBE,点D在AC上,BC与DE交于点P,若AD=DC=2.4,BC=4.1. 如图,在平面直角坐标系中,点A的坐标为(0,6),将△OAB沿x轴向左平移得到△O′A′B′,点A的对应点A′落在直线上y=-$\frac{3}{4}$x上,求点B与其对应点B′间的距离.
如图,在平面直角坐标系中,点A的坐标为(0,6),将△OAB沿x轴向左平移得到△O′A′B′,点A的对应点A′落在直线上y=-$\frac{3}{4}$x上,求点B与其对应点B′间的距离.