题目内容
17．
如图，直线l1∥l2，∠A=125°，∠B=105°，则∠1+∠2=50°．
分析 连结CD，如图，先利用四边形内角和为360°可计算出∠3+∠4=130°，然后根据两直线平行，同旁内角互补计算出∠1+∠2的度数．
解答 解：连结CD，如图，
∵四边形ABCD的内角和为360°，
∴∠3+∠4=360°-125°-105°=130°，
∵l1∥l2，
∴∠1+∠2+∠3+∠4=180°，
∴∠1+∠2=180°-130°=50°．
故答案为50．
点评 本题考查了平行线的性质：两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等．
练习册系列答案
相关题目
7．
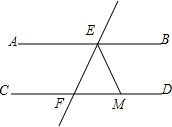已知：如图，AB∥CD，直线EF交AB于点E，交CD于点F，∠FEB的平分线交CD于点M，且∠CFE=120°，则∠EMF的度数为（ ）
已知：如图，AB∥CD，直线EF交AB于点E，交CD于点F，∠FEB的平分线交CD于点M，且∠CFE=120°，则∠EMF的度数为（ ）| A． | 30° | B． | 40° | C． | 120° | D． | 60° |
9．在Rt△ABC中，∠C=90°，$cosB=\frac{1}{2}$，则∠A的度数为（ ）
| A． | 15° | B． | 30° | C． | 45° | D． | 60° |
