题目内容
6.计算(1)3xy(x2y-$\frac{1}{3}$xy)
(2)x(x2-xy+y2)-y(x2+$\frac{1}{2}$xy+y2)
(3)t3-2t[t2-2(t-3)].
分析 (1)单项式与多项式相乘的运算法则:单项式与多项式相乘,就是用单项式去乘多项式的每一项,再把所得的积相加.依此计算即可求解.
(2)先算单项式乘多项式,再去括号,合并同类项即可求解;
(3)先算小括号,再算中括号,最后合并同类项即可求解.
解答 解:(1)3xy(x2y-$\frac{1}{3}$xy)=3x3y2-x2y2;
(2)x(x2-xy+y2)-y(x2+$\frac{1}{2}$xy+y2)
=(x3-x2y+xy2)-(x2y+$\frac{1}{2}$xy2+y3)
=x3-x2y+xy2-x2y-$\frac{1}{2}$xy2-y3
=x3-2x2y+$\frac{1}{2}$xy2-y3;
(3)t3-2t[t2-2(t-3)]
=t3-2t[t2-2t+6]
=t3-2t3+4t2-12t
=-t3+4t2-12t.
点评 考查了单项式乘多项式,单项式与多项式相乘时,应注意以下几个问题:
①单项式与多项式相乘实质上是转化为单项式乘以单项式;②用单项式去乘多项式中的每一项时,不能漏乘;③注意确定积的符号.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.计算2-2(1-a)的结果是( )
| A. | a | B. | -a | C. | 2a | D. | -2a |
15.下列计算正确的是( )
| A. | -x3+3x3=2x3 | B. | x+x=x2 | C. | x3+2x5=3x3 | D. | x5-x4=x |
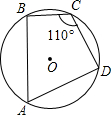 如图,四边形ABCD为⊙O的内接四边形,已知∠BCD=110°,则∠BAD=70度.
如图,四边形ABCD为⊙O的内接四边形,已知∠BCD=110°,则∠BAD=70度.
 在矩形纸片ABCD中,AE=CG=$\sqrt{3}$,点P,Q分别是在边AB,CD上,BP=DQ,将△BGP和△DEQ分别沿PG,EQ翻折,点D,B的对应点分别是D′,B′,若四边形ED′GB′是有一边平行于AB的菱形(如图甲或图乙所示),且∠D′EB′=30°,则AP的长是2$\sqrt{3}$+1或3.
在矩形纸片ABCD中,AE=CG=$\sqrt{3}$,点P,Q分别是在边AB,CD上,BP=DQ,将△BGP和△DEQ分别沿PG,EQ翻折,点D,B的对应点分别是D′,B′,若四边形ED′GB′是有一边平行于AB的菱形(如图甲或图乙所示),且∠D′EB′=30°,则AP的长是2$\sqrt{3}$+1或3.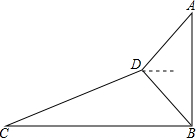 如图,小明为了测量大楼AB的高度,他从点C出发,沿着斜坡面CD走104米到点D处,测得大楼顶部点A的仰角为37°,大楼底部点B的俯角为45°,已知斜坡CD的坡度为i=1:2.4.(参考书据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
如图,小明为了测量大楼AB的高度,他从点C出发,沿着斜坡面CD走104米到点D处,测得大楼顶部点A的仰角为37°,大楼底部点B的俯角为45°,已知斜坡CD的坡度为i=1:2.4.(参考书据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)