题目内容
4．已知分式$\frac{x-3}{{x}^{2}-5x+a}$，当x=2时，分式无意义，则a=6；当x=0时，使分式无意义的a的值为0．分析 根据分式无意义，分母等于0分别列方程求解即可．
解答 解：x=2时，∵分式无意义，
∴4-10+a=0，
解得a=6；
x=0时，∵分式无意义，
∴0-0+a=0，
解得a=0．
故答案为：6，0．
点评 本题考查了分式有意义的条件，从以下三个方面透彻理解分式的概念：
（1）分式无意义?分母为零；
（2）分式有意义?分母不为零；
（3）分式值为零?分子为零且分母不为零．
练习册系列答案
挑战100单元检测试卷系列答案
相关题目
15．下列说法正确的是（ ）
| A． | “购买一张彩票就中奖”是不可能事件 | |
| B． | “抛掷一枚质地均匀的骰子，向上一面的点数是6”是随机事件 | |
| C． | 了解我国青年人喜欢的电视节目应做普查 | |
| D． | 从扇形统计图中，可以直接得到各部分的具体数值 |
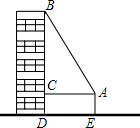如图，一高层住宅发生火灾，消防车立即赶到距大厦5米处（车尾AE到大厦墙面CD的距离为5米），升起云梯到火灾窗口B，已知云梯AB长13米，云梯底部距地面的高AE为3米，求发生火灾的住户窗口距地面的高BD是多少米？
19．当a=-2时，下列运算中，错误的是（ ）
| A． | $\frac{1}{a}$•a=1 | B． | |a-2|+|a+1|=5 | C． | -a3+a+（-a）2=10 | D． | $\frac{1}{a}$-$\frac{1}{{a}^{2}}$=$\frac{1}{4}$ |
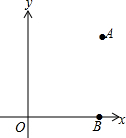如图，在平面直角坐标系xOy中点A（6，8），点B（6，0）．