题目内容
19. 如图,长方体盒子是用大长方形硬纸片裁剪制作的,每个盒子由4个小长方形侧面和上下2个正方形底面组成,大长方形硬纸片按两种方法裁剪:A所示方法剪4个侧面:B所示方法剪6个底面.现有112张大长方形硬纸片全部用于裁剪制作长方体盒子,设裁剪时x张用A方法,其余用B方法.
如图,长方体盒子是用大长方形硬纸片裁剪制作的,每个盒子由4个小长方形侧面和上下2个正方形底面组成,大长方形硬纸片按两种方法裁剪:A所示方法剪4个侧面:B所示方法剪6个底面.现有112张大长方形硬纸片全部用于裁剪制作长方体盒子,设裁剪时x张用A方法,其余用B方法.(1)请用含x的代数式分别表示裁剪出的侧面和底面个数;
(2)若裁剪出的侧面和底面恰好全部用完,问A方法、B方法各裁剪几张?能做多少个盒子?
分析 (1)根据题意可以分别用代数式表示出裁剪出的侧面和底面个数;
(2)根据题意可以列出相应的方程,从而可以解答本题.
解答 解:(1)由题意可得,
裁剪出的侧面个数是:4x,
裁剪出的底面个数是:6(112-x)=-6x+672;
(2)由题意可得,
4x=2×(-6x+672),
解得,x=84,
∴112-84=28,
即A方法裁剪84张,B方法裁剪28张,能做84个盒子.
点评 本题考查一元一次方程的应用,解答本题的关键是明确题意,找出等量关系,侧面的个数是底面个数的2倍,利用方程的思想解答.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
16. 如图,直线l1∥l2,CD⊥AB于点D,∠1=40°,则∠2的度数为( )
如图,直线l1∥l2,CD⊥AB于点D,∠1=40°,则∠2的度数为( )
 如图,直线l1∥l2,CD⊥AB于点D,∠1=40°,则∠2的度数为( )
如图,直线l1∥l2,CD⊥AB于点D,∠1=40°,则∠2的度数为( )| A. | 50° | B. | 45° | C. | 40° | D. | 30° |
10.若2x=4y+1,27y=3x+1,则x-y等于( )
| A. | 5 | B. | -3 | C. | -1 | D. | 1 |
14.已知a-b=2,则a2-4b-b2的值是( )
| A. | 0 | B. | 2 | C. | 4 | D. | 6 |
11. 如图,在平行四边形ABCD中,点E在AD上,连接CE并延长与BA的延长线交于点F,若AE=2ED,则下列结论错误的是( )
如图,在平行四边形ABCD中,点E在AD上,连接CE并延长与BA的延长线交于点F,若AE=2ED,则下列结论错误的是( )
 如图,在平行四边形ABCD中,点E在AD上,连接CE并延长与BA的延长线交于点F,若AE=2ED,则下列结论错误的是( )
如图,在平行四边形ABCD中,点E在AD上,连接CE并延长与BA的延长线交于点F,若AE=2ED,则下列结论错误的是( )| A. | EF=2CE | B. | S△AEF=$\frac{2}{3}$S△BCF | C. | BF=3CD | D. | BC=$\frac{3}{2}$AE |
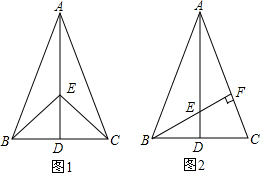
 如图,在△ABC中,BD=CD,∠1=∠2,小颖说:“AD⊥BC”,你认为她说的对吗?说明你的理由.
如图,在△ABC中,BD=CD,∠1=∠2,小颖说:“AD⊥BC”,你认为她说的对吗?说明你的理由. 如图所示.在平面直角坐标系xOy中,点A坐标为(6,6).作正方形OBAC,点D坐标为(8,2),作正方形BEDF.连结OA,EF.点P,Q,R分别为OA,EF,OF的中点,连结PQ,PR,QR.
如图所示.在平面直角坐标系xOy中,点A坐标为(6,6).作正方形OBAC,点D坐标为(8,2),作正方形BEDF.连结OA,EF.点P,Q,R分别为OA,EF,OF的中点,连结PQ,PR,QR.