题目内容
16.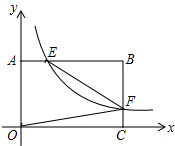 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象与矩形OABC的边AB、BC分别交于点E、F,若S矩形OABC=2,则当k=1时,四边形OAEF的面积最大.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象与矩形OABC的边AB、BC分别交于点E、F,若S矩形OABC=2,则当k=1时,四边形OAEF的面积最大.
分析 设B(a,b),则ab=2,根据反比例函数图象上点的坐标特征得E($\frac{k}{b}$,b),F(a,$\frac{k}{a}$),所以BE=a-$\frac{k}{b}$,BF=b-$\frac{k}{a}$,根据三角形面积公式和反比例函数系数k的几何意义,利用四边形OAEF的面积=S矩形ABCO-S△OCF-S△BEF得到四边形OAEF的面积=-$\frac{1}{4}$k2+$\frac{1}{2}$k+1,然后根据二次函数的最值问题求解.
解答 解:设B(a,b),则ab=2,E($\frac{k}{b}$,b),F(a,$\frac{k}{a}$),
∴BE=a-$\frac{k}{b}$,BF=b-$\frac{k}{a}$,
四边形OAEF的面积=S矩形ABCO-S△OCF-S△BEF
=2-$\frac{1}{2}$k-$\frac{1}{2}$(a-$\frac{k}{b}$)(b-$\frac{k}{a}$)
=-$\frac{1}{4}$k2+$\frac{1}{2}$k+1,
当k=-$\frac{\frac{1}{2}}{2×(-\frac{1}{4})}$=1时,四边形OAEF的面积最大.
故答案为1.
点评 本题考查了反比例函数系数k的几何意义:在反比例函数y=$\frac{k}{x}$图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.在反比例函数的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是$\frac{1}{2}$|k|,且保持不变.

练习册系列答案
相关题目
 如图,由几个相同的小正方体搭成的一个几何体,它的俯视图为( )
如图,由几个相同的小正方体搭成的一个几何体,它的俯视图为( )



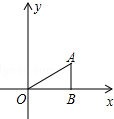 如图,△ABO中,AB⊥OB,OB=$\sqrt{3}$,AB=1,把△ABO绕点O逆时针旋转120°后得到△A1B1O,则点B1的坐标为(-$\frac{\sqrt{3}}{2}$,$\frac{3}{2}$).
如图,△ABO中,AB⊥OB,OB=$\sqrt{3}$,AB=1,把△ABO绕点O逆时针旋转120°后得到△A1B1O,则点B1的坐标为(-$\frac{\sqrt{3}}{2}$,$\frac{3}{2}$).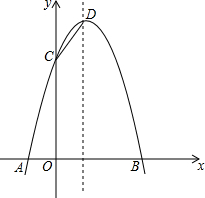 如图,已知抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3).
如图,已知抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3).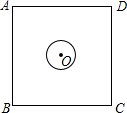 如图,圆心O恰好为正方形ABCD的中心,已知AB=10,⊙O的半径为1,现将⊙O在正方形内部沿某一方向平移,当它与正方形ABCD的某条边相切时停止平移,设此时的平移的距离为d,则d的取值范围是4≤d$≤4\sqrt{2}$.
如图,圆心O恰好为正方形ABCD的中心,已知AB=10,⊙O的半径为1,现将⊙O在正方形内部沿某一方向平移,当它与正方形ABCD的某条边相切时停止平移,设此时的平移的距离为d,则d的取值范围是4≤d$≤4\sqrt{2}$. 如图:E,F,M,N分别是菱形ABCD四边上的中点.
如图:E,F,M,N分别是菱形ABCD四边上的中点.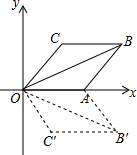 如图,菱形OABC的一边OA在x轴上,将菱形OABC沿x轴翻折到四边形OAB′C′的位置,若OB=2$\sqrt{3}$,∠C=120°,则点B′的坐标为(3,$-\sqrt{3}$).
如图,菱形OABC的一边OA在x轴上,将菱形OABC沿x轴翻折到四边形OAB′C′的位置,若OB=2$\sqrt{3}$,∠C=120°,则点B′的坐标为(3,$-\sqrt{3}$).