题目内容
5. 如图:E,F,M,N分别是菱形ABCD四边上的中点.
如图:E,F,M,N分别是菱形ABCD四边上的中点.(1)试判断四边形EFMN是什么图形,并证明你的结论;
(2)如果菱形边长为4,∠B=60°,根据(1)试求四边形EFMN的周长;
(3)当四边形ABCD满足什么条件时四边形EFMN是菱形.
分析 (1)首先连接AC、BD.要证四边形EFMN是矩形,只要证得NE⊥NM即可.先由菱形的对角线互相垂直,得AC⊥BD,再结合题意证得四边形EFMN是平行四边形,利用平行四边形的性质,易证NE⊥NM,从而证得四边形EFMN是矩形;
(2)利用菱形的性质结合直角三角形的性质分别得出EF,EN的长即可得出答案;
(3)利用菱形的判定方法结合中点四边形的性质得出答案.
解答 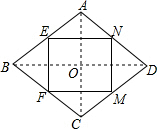 解:(1)四边形EFMN是矩形;
解:(1)四边形EFMN是矩形;
理由:连接AC、BD,
∵AC⊥BD,
∴E,F,M,N分别是菱形ABCD四条边的中点.
∴NE∥BD,MF∥BD.
∴NE∥MF.
同理,得:NM∥AC,EF∥AC.
∴NM∥EF.
∴四边形EFMN是平行四边形.
∵NE∥BD,AC⊥BD,
∴NE⊥AC.
∵NM∥AC,
∴NE⊥NM.
∴平行四边形EFMN是矩形;
(2)∵菱形ABCD边长为4,∠B=60°,
∴AB=BC=4,
∴△ABC是等边三角形,
∴AC=4,
则EF=MN=2,
∵菱形ABCD边长为4,∠B=60°,
∴∠ABD=30°,则AO=2,
∴BO=2$\sqrt{3}$,
∴BD=4$\sqrt{3}$,EN=FM=2$\sqrt{3}$,
∴四边形EFMN的周长为:2+2+2$\sqrt{3}$+2$\sqrt{3}$=4+4$\sqrt{3}$;
(3)当四边形ABCD满足AC=BD时,四边形EFMN是菱形.
理由:E,F,M,N分别是四边形ABCD四条边的中点,
∴NE∥BD,MF∥BD.
∴NE∥MF.
同理,得:NM∥AC,EF∥AC.
∴NM∥EF.
∴四边形EFMN是平行四边形.
∵NE$\stackrel{∥}{=}$$\frac{1}{2}$BD,FE$\stackrel{∥}{=}$$\frac{1}{2}$AC,
∴EN=EF,
∴平行四边形EFMN是菱形.
点评 此题主要考查了菱形以及矩形的判定方法,熟练掌握中点四边形的性质结合三角形中位线定理得出是解题关键.

 如图,已知三角形ABC平移后得到三角形DEF,则下列说法中,不正确的是( )
如图,已知三角形ABC平移后得到三角形DEF,则下列说法中,不正确的是( )| A. | AC=DF | B. | BC∥EF | ||
| C. | 平移的距离是线段BD的长 | D. | 平移的距离是线段AD的长 |
| A. | 2是(-2)2的算术平方根 | B. | -2是-4的平方根 | ||
| C. | (-2)2的平方根是2 | D. | 8的立方根是±2 |
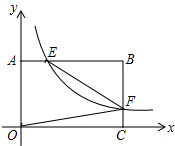 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象与矩形OABC的边AB、BC分别交于点E、F,若S矩形OABC=2,则当k=1时,四边形OAEF的面积最大.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象与矩形OABC的边AB、BC分别交于点E、F,若S矩形OABC=2,则当k=1时,四边形OAEF的面积最大. 如图,在平面直角坐标系中,矩形OABC的顶点B坐标为(8,4),将矩形OABC绕点O逆时针旋转,使点B落在y轴上的点B′处,得到矩形OA′B′C′,OA′与BC相交于点D,则经过点D的反比例函数解析式是y=$\frac{8}{x}$.
如图,在平面直角坐标系中,矩形OABC的顶点B坐标为(8,4),将矩形OABC绕点O逆时针旋转,使点B落在y轴上的点B′处,得到矩形OA′B′C′,OA′与BC相交于点D,则经过点D的反比例函数解析式是y=$\frac{8}{x}$.
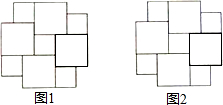 如图是以两个大小不同的正方形为基本图案镶嵌而成的图形,请仅用无刻度的直尺按不同的方法分别在图1、图2中画一个正方形,使它的面积等于这两个大小不同的正方形的面积之和.要求:(1)用虚线连线;(2)要标注你所画正方形的顶点字母.
如图是以两个大小不同的正方形为基本图案镶嵌而成的图形,请仅用无刻度的直尺按不同的方法分别在图1、图2中画一个正方形,使它的面积等于这两个大小不同的正方形的面积之和.要求:(1)用虚线连线;(2)要标注你所画正方形的顶点字母.