题目内容
1.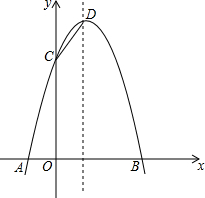 如图,已知抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3).
如图,已知抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3).(1)求抛物线的解析式;
(2)设抛物线的顶点为D,在其对称轴的右侧的抛物线上是否存在点P,使得△PDC是等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由:
分析 (1)根据待定系数法,可得函数解析式;
(2)根据等腰三角形的判定,可得三角形三边的关系,分类讨论:PD=CD,根据勾股定理,可得x2+(3-y)2=(x-1)2+(4-y)2,根据图象上的点满足函数解析式,可得关于x的方程,根据解方程,可得答案;PD=CD时,根据对称性,可得答案.
解答 解:(1)∵抛物线与y轴交于点C(0,3),
∴设抛物线解析式为y=ax2+bx+3,
根据题意,得$\left\{\begin{array}{l}{a-b+3=0}\\{9a+3b+3=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-1}\\{b=2}\end{array}\right.$,
∴抛物线的解析式为y=-x2+2x+3.
(2)存在点P,使得△PDC是等腰三角形.
由y=-x2+2x+3,得
D点坐标为(1,4),对称轴为x=1,
①若以CD为底边,则PD=PC,设P点坐标为(x,y),
根据勾股定理,得x2+(3-y)2=(x-1)2+(4-y)2,即y=4-x.
又P点(x,y)在抛物线上,
∴4-x=-x2+2x+3,即x2-3x+1=0,
解得:x=$\frac{3±\sqrt{5}}{2}$,x=$\frac{3-\sqrt{5}}{2}$<1 (不合题意,舍去),
所以x=$\frac{3+\sqrt{5}}{2}$,y=4-x=$\frac{5-\sqrt{5}}{2}$,
即点P的坐标为($\frac{3+\sqrt{5}}{2}$,$\frac{5-\sqrt{5}}{2}$);
②若以CD为一腰,PD=CD,因为点P在对称轴右侧的抛物线上,
由抛物线对称性知,点P与点C关于直线x=1对称,此时点P坐标为(2,3),
综上所述:符合条件的点P坐标为($\frac{3+\sqrt{5}}{2}$,$\frac{5-\sqrt{5}}{2}$) 或(2,3).
点评 本题考查了二次函数综合题,利用待定系数法求函数解析式,等腰三角形的判定,勾股定理,函数图象的对称性,分类讨论是解题关键,以防遗漏.

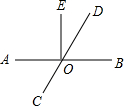 如图,直线AB,CD相交于点O,OE⊥AB,O为垂足,∠EOD=30°,则∠AOC=60°.
如图,直线AB,CD相交于点O,OE⊥AB,O为垂足,∠EOD=30°,则∠AOC=60°.
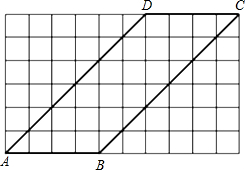 如图,在正方形网格中有一个边长为4的平行四边形ABCD
如图,在正方形网格中有一个边长为4的平行四边形ABCD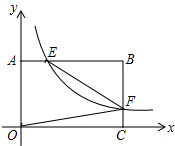 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象与矩形OABC的边AB、BC分别交于点E、F,若S矩形OABC=2,则当k=1时,四边形OAEF的面积最大.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象与矩形OABC的边AB、BC分别交于点E、F,若S矩形OABC=2,则当k=1时,四边形OAEF的面积最大. 在平面直角坐标系xOy中,给出如下定义:形如y=a(x-m)2+a(x-m)与y=a(x-m)2-a(x-m)的两个二次函数的图象叫做“兄弟抛物线”.
在平面直角坐标系xOy中,给出如下定义:形如y=a(x-m)2+a(x-m)与y=a(x-m)2-a(x-m)的两个二次函数的图象叫做“兄弟抛物线”. 如图,在平面直角坐标系中,矩形OABC的顶点B坐标为(8,4),将矩形OABC绕点O逆时针旋转,使点B落在y轴上的点B′处,得到矩形OA′B′C′,OA′与BC相交于点D,则经过点D的反比例函数解析式是y=$\frac{8}{x}$.
如图,在平面直角坐标系中,矩形OABC的顶点B坐标为(8,4),将矩形OABC绕点O逆时针旋转,使点B落在y轴上的点B′处,得到矩形OA′B′C′,OA′与BC相交于点D,则经过点D的反比例函数解析式是y=$\frac{8}{x}$.