题目内容
6.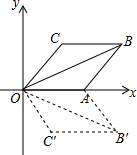 如图,菱形OABC的一边OA在x轴上,将菱形OABC沿x轴翻折到四边形OAB′C′的位置,若OB=2$\sqrt{3}$,∠C=120°,则点B′的坐标为(3,$-\sqrt{3}$).
如图,菱形OABC的一边OA在x轴上,将菱形OABC沿x轴翻折到四边形OAB′C′的位置,若OB=2$\sqrt{3}$,∠C=120°,则点B′的坐标为(3,$-\sqrt{3}$).
分析 由∠C=120°可求得∠COA=60°,由菱形的性质可知:∠BOA=30°,由OB=2$\sqrt{3}$,从可求得点B的横纵坐标,最后根据关于x轴对称点的坐标特点可知求得点B′的坐标.
解答 解:∵四边形OABC是菱形,
∴∠C+∠COA=180°,
∴∠COA=180°-120°=60°.
由菱形的性质可知:∠BOA=30°,
∴点B的横坐标=OB•cos30°=2$\sqrt{3}×\frac{\sqrt{3}}{2}$=3,点B的纵坐标=OB•sin30°=2$\sqrt{3}×\frac{1}{2}$=$\sqrt{3}$.
由关于x轴对称点的坐标特点可知:点B′(3,$-\sqrt{3}$).
故答案为:(3,$-\sqrt{3}$).
点评 本题主要考查的是菱形的性质、翻折变换和特殊锐角三角函数值,根据菱形的性质求得∠BOA=30°是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.五莲花联商店需要购进一批电视机和洗衣机,根据市场调查,决定电视机进货量不少于洗衣机货量的一半,电视机与洗衣机的进价和售价如下表:
计划购进电视机和洗衣机共120台,商店最多可筹集资金193500元.
(1)请你帮助商店算一算有多少种进货方案?(不考虑除进价以外的其他费用)
(2)哪种进货方案待商店销售购进的电视机与洗衣机完毕后获得利润最多?并求出最大的利润.(利润=售价-进价)(要求:请用函数的思想来完成此题).
| 类别 | 进价(元/台) | 洗衣机 |
| 进价(元/台) | 1800 | 1500 |
| 售价(元/台) | 2000 | 1600 |
(1)请你帮助商店算一算有多少种进货方案?(不考虑除进价以外的其他费用)
(2)哪种进货方案待商店销售购进的电视机与洗衣机完毕后获得利润最多?并求出最大的利润.(利润=售价-进价)(要求:请用函数的思想来完成此题).
15.下列说法正确的是( )
| A. | 2是(-2)2的算术平方根 | B. | -2是-4的平方根 | ||
| C. | (-2)2的平方根是2 | D. | 8的立方根是±2 |
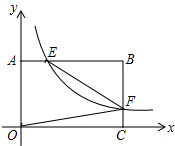 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象与矩形OABC的边AB、BC分别交于点E、F,若S矩形OABC=2,则当k=1时,四边形OAEF的面积最大.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象与矩形OABC的边AB、BC分别交于点E、F,若S矩形OABC=2,则当k=1时,四边形OAEF的面积最大.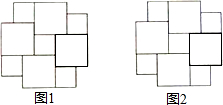 如图是以两个大小不同的正方形为基本图案镶嵌而成的图形,请仅用无刻度的直尺按不同的方法分别在图1、图2中画一个正方形,使它的面积等于这两个大小不同的正方形的面积之和.要求:(1)用虚线连线;(2)要标注你所画正方形的顶点字母.
如图是以两个大小不同的正方形为基本图案镶嵌而成的图形,请仅用无刻度的直尺按不同的方法分别在图1、图2中画一个正方形,使它的面积等于这两个大小不同的正方形的面积之和.要求:(1)用虚线连线;(2)要标注你所画正方形的顶点字母.