题目内容
4.已知A,B,C三个圆柱形容器的底面积之比为1:2:3,且容器的高都为10cm,若A,B,C三个容器中分别装有液面高度为6cm、8cm、6cm的液体,现把C容器中的液体分别倒入A,B两个容器中,直至装满这两个容器(无溢出),此时C容器中还剩120cm3的液体.(1)若设A容器的底面积为x(cm2),请用含x的代数式表示三个容器中液体的总体积;
(2)求C容器的体积;
(3)若A,B,C三个容器中的液体可互相倒入(无溢出),最后是否能使三个容器中的液体体积都相等?若能,求出每个容器中的液体体积;若不能,说明理由.
分析 (1)根据圆柱的体积等于底面积乘高求解即可;
(2)根据液体的体积不变列出关于x的方程,求得x的值,最后用底面积乘高计算即可;
(3)由(1)可知液体的总体积为40xcm3,A容器的容积为10xcm3,10xcm3<$\frac{40x}{3}$10xcm3,从而可判断.
解答 解:(1)A容器的底面积为x(cm2),则B容器的底面积为2x(cm2),C容器的底面积为3x(cm2).
三个容器中液体的总体积=6x+2x×8+3x×6=6x+16x+18x=40x.
(2)根据题意得:40x=10x+2x×10+120.
解得:x=12cm2.
C容器的体积=10×3x=10×3×12=360cm3.
(3)不能.
理由:A容器的体积为10xcm3,液体的总体积为40xcm3,.
40x÷3=$\frac{40x}{3}$>10x.
所以不能够.
点评 本题主要考查的是一元一次方程的应用,根据三个容器中液体的体积不变列出方程是解题的关键.

练习册系列答案
相关题目
19.下列各式不正确的是( )
| A. | 18000″<360′ | B. | 2°30′>2.4° | C. | 36000″<8° | D. | 1°10′20″>4219″ |
16.甲、乙、丙、丁四名选手参加100米决赛,赛场设1,2,3,4四个跑道,选手以抽签的方式决定自己的跑道,若甲第一个抽签,乙第二个抽签,则甲抽到1号跑道,乙抽到2号跑道的概率是( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{12}$ | D. | $\frac{1}{16}$ |
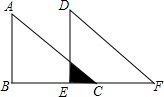 如图,等腰直角三角形ABC中,∠ABC=90°,AB=BC=4cm,将△ABC沿BC方向平移3cm后,得△DEF,则图中阴影部分的面积为$\frac{1}{2}$cm2.
如图,等腰直角三角形ABC中,∠ABC=90°,AB=BC=4cm,将△ABC沿BC方向平移3cm后,得△DEF,则图中阴影部分的面积为$\frac{1}{2}$cm2. 如图,等边三角形ABC中,BD是AC边上的中线,BD=BE,则∠EDA=15 度.
如图,等边三角形ABC中,BD是AC边上的中线,BD=BE,则∠EDA=15 度.