题目内容
14.Rt△ABC,∠ACB=90°,∠A:∠B=1:2,则$\frac{AC}{AB}$=$\frac{\sqrt{3}}{2}$.分析 根据在Rt△ABC,∠ACB=90°,∠A:∠B=1:2,可以得到∠A,∠B的度数,从而可以解答本题.
解答 解:∵在Rt△ABC,∠ACB=90°,∠A:∠B=1:2,
∴∠A+∠B=90°.
∴∠A=30°,∠B=60°.
∵sinB=$\frac{AC}{AB}$,∠B=60°,
∴$\frac{AC}{AB}=\frac{\sqrt{3}}{2}$.
故答案为:$\frac{\sqrt{3}}{2}$.
点评 本题考查解直角三角形,解题的关键知道特殊角的锐角三角函数,找出所求问题需要的条件.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
6.已知代数式x+2y的值是3,则代数式2x+4y+2010的值是( )
| A. | 2013 | B. | 2014 | C. | 2015 | D. | 2016 |
4.若-6xayzb与9x3ycz2是同类项,则a、b、c的值分别是( )
| A. | a=1,b=2,c=3 | B. | a=3,b=1,c=2 | C. | a=3,b=2,c=1 | D. | 以上都不对 |
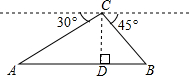 如图,从坡顶C处测得地面A、B两点的俯角分别为30°、45°,如果此时C出的高度CD为150米,且点A、D、B在同一直线上,则AB两点间距离是(150$\sqrt{3}$+150)米.
如图,从坡顶C处测得地面A、B两点的俯角分别为30°、45°,如果此时C出的高度CD为150米,且点A、D、B在同一直线上,则AB两点间距离是(150$\sqrt{3}$+150)米. 如图,在?ABCD中,EF∥AB,FG∥ED,DE:DA=2:5,EF=4,求线段CG的长.
如图,在?ABCD中,EF∥AB,FG∥ED,DE:DA=2:5,EF=4,求线段CG的长.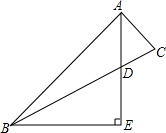 已知:如图,在△ABC中,AB=3AC,AD平分∠BAC,BE⊥AD交AD的延长线于点E.设△ACD的面积是S.
已知:如图,在△ABC中,AB=3AC,AD平分∠BAC,BE⊥AD交AD的延长线于点E.设△ACD的面积是S.