题目内容
9.不等式组$\left\{\begin{array}{l}{x+2≤3}\\{\frac{-2x+3}{3}<3}\end{array}\right.$的解集在数轴上表示为( )| A. |  | B. |  | ||
| C. | 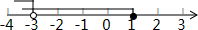 | D. |  |
分析 先求出不等式组中每一个不等式的解集,再求出它们的公共部分,然后把不等式的解集表示在数轴上即可.
解答 解:$\left\{\begin{array}{l}{x+2≤3}\\{\frac{-2x+3}{3}<3}\end{array}\right.$,
由x+2≤3得x≤1,
由$\frac{-2x+3}{3}$<3得x>-3,
则不等式组的解集为-3<x≤1,
在数轴上表示为:
故选A.
点评 考查了解一元一次不等式组,在数轴上表示不等式的解集,把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),数轴上的点把数轴分成若干段,如果数轴的某一段上面表示解集的线的条数与不等式的个数一样,那么这段就是不等式组的解集.有几个就要几个.在表示解集时“≥”,“≤”要用实心圆点表示;“<”,“>”要用空心圆点表示.

练习册系列答案
相关题目
20.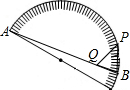 如图,点A是量角器直径的一个端点,点B在半圆周上,点P在$\widehat{AB}$上,点Q在AB上,且PB=PQ.若点P对应140°(40°),则∠PQB的度数为( )
如图,点A是量角器直径的一个端点,点B在半圆周上,点P在$\widehat{AB}$上,点Q在AB上,且PB=PQ.若点P对应140°(40°),则∠PQB的度数为( )
 如图,点A是量角器直径的一个端点,点B在半圆周上,点P在$\widehat{AB}$上,点Q在AB上,且PB=PQ.若点P对应140°(40°),则∠PQB的度数为( )
如图,点A是量角器直径的一个端点,点B在半圆周上,点P在$\widehat{AB}$上,点Q在AB上,且PB=PQ.若点P对应140°(40°),则∠PQB的度数为( )| A. | 65° | B. | 70° | C. | 75° | D. | 80° |
4.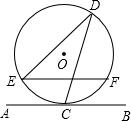 如图,直线AB与半径为2的⊙O相切于点C,点D、E、F是⊙O上三个点,EF∥AB,若EF=2$\sqrt{3}$,则∠EDC的度数为( )
如图,直线AB与半径为2的⊙O相切于点C,点D、E、F是⊙O上三个点,EF∥AB,若EF=2$\sqrt{3}$,则∠EDC的度数为( )
 如图,直线AB与半径为2的⊙O相切于点C,点D、E、F是⊙O上三个点,EF∥AB,若EF=2$\sqrt{3}$,则∠EDC的度数为( )
如图,直线AB与半径为2的⊙O相切于点C,点D、E、F是⊙O上三个点,EF∥AB,若EF=2$\sqrt{3}$,则∠EDC的度数为( )| A. | 60° | B. | 90° | C. | 30° | D. | 75° |
18.下列命题中,属于真命题的是( )
| A. | 各边相等的多边形是正多边形 | B. | 同角或等角的余角相等 | ||
| C. | 必然事件发生的概率为0 | D. | 六边形的内角和等于540° |
19.2013年,广东全年实现地区生产总值62200亿元,同比增长8.5%,数据62200亿用科学记数法表示正确的是( )
| A. | 6.22×104亿 | B. | 0.622×105亿 | C. | 6.22×105亿 | D. | 62.2×103亿 |
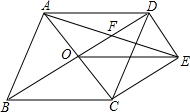 如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=$\frac{1}{2}$AC,连接AE交OD于点F,连接CE、OE.
如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=$\frac{1}{2}$AC,连接AE交OD于点F,连接CE、OE.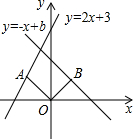 如图,在平面直角坐标系中,点A(-1,m)在直线y=2x+3上,连接OA,将线段OA绕点O顺时针旋转90°,点A的对应点B恰好落在直线y=-x+b上,则b的值为2.
如图,在平面直角坐标系中,点A(-1,m)在直线y=2x+3上,连接OA,将线段OA绕点O顺时针旋转90°,点A的对应点B恰好落在直线y=-x+b上,则b的值为2.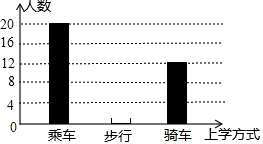 学习了统计知识后,小明就本班同学的上学方式进行了一次调查统计,他通过采集数据后,绘制一幅不完整的统计图(如图所示).已知骑车的人数占全班人数的30%,结合图中提供的信息,可得该班步行上学的有8人.
学习了统计知识后,小明就本班同学的上学方式进行了一次调查统计,他通过采集数据后,绘制一幅不完整的统计图(如图所示).已知骑车的人数占全班人数的30%,结合图中提供的信息,可得该班步行上学的有8人.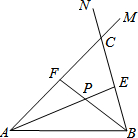 在线段AB的同侧作射线AM和BN,若∠MAB与∠NBA的平分线分别交射线BN,AM于点E,F,AE和BF交于点P.如图,点点同学发现当射线AM,BN交于点C;且∠ACB=60°时,有以下两个结论:
在线段AB的同侧作射线AM和BN,若∠MAB与∠NBA的平分线分别交射线BN,AM于点E,F,AE和BF交于点P.如图,点点同学发现当射线AM,BN交于点C;且∠ACB=60°时,有以下两个结论: