题目内容
18.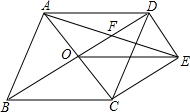 如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=$\frac{1}{2}$AC,连接AE交OD于点F,连接CE、OE.
如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DE∥AC且DE=$\frac{1}{2}$AC,连接AE交OD于点F,连接CE、OE.(1)求证:OE=CD;
(2)若菱形ABCD的边长为2,∠ABC=60°,求AE的长.
分析 (1)由菱形ABCD中,DE∥AC且DE=$\frac{1}{2}$AC,易证得四边形OCED是平行四边形,继而可得OE=CD即可;
(2)由菱形的对角线互相垂直,可证得四边形OCED是矩形,根据菱形的性质得出AC=AB,再根据勾股定理得出AE的长度即可.
解答 (1)证明:四边形ABCD是菱形,
∴OA=OC=$\frac{1}{2}$AC,AD=CD,
∵DE∥AC且DE=$\frac{1}{2}$AC,
∴DE=OA=OC,
∴四边形OADE、四边形OCED都是平行四边形,
∴OE=AD,
∴OE=CD;
(2)解:∵AC⊥BD,
∴四边形OCED是矩形,
∵在菱形ABCD中,∠ABC=60°,
∴AC=AB=2,
∴在矩形OCED中,CE=OD=$\sqrt{A{D}^{2}-A{O}^{2}}$=$\sqrt{3}$.
∴在Rt△ACE中,AE=$\sqrt{A{C}^{2}+C{E}^{2}}$=$\sqrt{7}$.
点评 本题考查了菱形的性质,矩形的判定与性质,勾股定理的应用.注意证得四边形OCED是平行四边形,四边形OCED是矩形是关键.

练习册系列答案
相关题目
8.下列二次根式中,最简二次根式是( )
| A. | $\sqrt{9}$ | B. | $\sqrt{20}$ | C. | $\sqrt{\frac{1}{3}}$ | D. | $\sqrt{7}$ |
9.下列各式计算正确的是( )
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 4$\sqrt{3}$-3$\sqrt{4}$=1 | C. | 2$\sqrt{3}$×3$\sqrt{3}$=6 | D. | $\sqrt{27}$÷$\sqrt{3}$=3 |
11.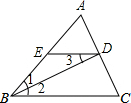 如图,△ABC中,BA=BC,BD是三角形的角平分线,DE∥BC交AB于E,下列结论:①∠1=∠3;②DE=$\frac{1}{2}$AB;③S△ADE=$\frac{1}{4}$S△ABC.正确的有( )
如图,△ABC中,BA=BC,BD是三角形的角平分线,DE∥BC交AB于E,下列结论:①∠1=∠3;②DE=$\frac{1}{2}$AB;③S△ADE=$\frac{1}{4}$S△ABC.正确的有( )
 如图,△ABC中,BA=BC,BD是三角形的角平分线,DE∥BC交AB于E,下列结论:①∠1=∠3;②DE=$\frac{1}{2}$AB;③S△ADE=$\frac{1}{4}$S△ABC.正确的有( )
如图,△ABC中,BA=BC,BD是三角形的角平分线,DE∥BC交AB于E,下列结论:①∠1=∠3;②DE=$\frac{1}{2}$AB;③S△ADE=$\frac{1}{4}$S△ABC.正确的有( )| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
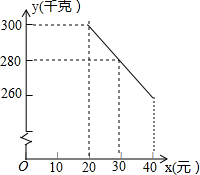 草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.
草莓是云南多地盛产的一种水果,今年某水果销售店在草莓销售旺季,试销售成本为每千克20元的草莓,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象.
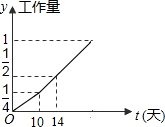 甲、乙两个工程队完成某项工程,首先是甲单独做了10天,然后乙队加入合做,完成剩下的全部工程,设工程总量为单位1,工程进度满足如图所示的函数关系,那么实际完成这项工程所用的时间比由甲单独完成这项工程所需时间少( )
甲、乙两个工程队完成某项工程,首先是甲单独做了10天,然后乙队加入合做,完成剩下的全部工程,设工程总量为单位1,工程进度满足如图所示的函数关系,那么实际完成这项工程所用的时间比由甲单独完成这项工程所需时间少( )