题目内容
如图,已知直线l:y=kx+b(k<0,b>0,且k、b为常数)与y轴、x轴分别交于A点、B点,双曲线C:y=
(x>0).
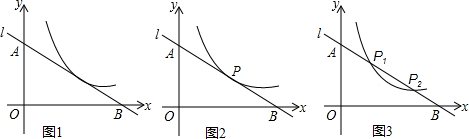
(1)当k=-1,b=2
时,求直线l与双曲线C公共点的坐标;
(2)当b=2
时,求证:不论k为任何小于零的实数,直线l与双曲线C只有一个公共点(设为P),并求公共点P的坐标(用k的式子表示).
(3)①在(2)的条件下,试猜想线段PA、PB是否相等.若相等,请加以证明;若不相等,请说明理由;
②若直线l与双曲线C相交于两点P1、P2,猜想并证明P1A与P2B之间的数量关系.
| 3 |
| x |

(1)当k=-1,b=2
| 3 |
(2)当b=2
| -3k |
(3)①在(2)的条件下,试猜想线段PA、PB是否相等.若相等,请加以证明;若不相等,请说明理由;
②若直线l与双曲线C相交于两点P1、P2,猜想并证明P1A与P2B之间的数量关系.
考点:反比例函数综合题
专题:
分析:(1)根据联立函数解析式,可得方程组,根据代入消元法,可得方程组的解,可得交点的坐标;
(2)根据联立函数解析式,可得方程组,根据代入消元法,可的一元二次方程,根据判别式,可得答案;
(3)①根据函数与自变量的关系,可得A、B点坐标,根据两点间距离公式,可得答案;
②根据函数与自变量的关系,可得A、B点坐标,根据联立函数解析式,可得方程组,根据代入消元法,可得方程组的解,可得交点的坐标,根据两点间距离公式,可得答案.
(2)根据联立函数解析式,可得方程组,根据代入消元法,可的一元二次方程,根据判别式,可得答案;
(3)①根据函数与自变量的关系,可得A、B点坐标,根据两点间距离公式,可得答案;
②根据函数与自变量的关系,可得A、B点坐标,根据联立函数解析式,可得方程组,根据代入消元法,可得方程组的解,可得交点的坐标,根据两点间距离公式,可得答案.
解答:解:(1)联立l与C得
,
①-②,得-x+2
-
=0
化简,得x2-2
x+3=0
解得x1=x2=
,y1=y2=
,
直线l与双曲线C公共点的坐标为(
,
);
(2)证明:联立l与C得
,
①-②,得
kx+2
-
=0,
化简,得
kx2+2
x-3=0,
a=k,b=2
,c=-3,
△=b2-4ac=(2
)2-4k×(-3)=12k-12k=0,
∴kx2+2
x-3=0只有相等两实根,即不论k为任何小于零的实数,直线l与双曲线C只有一个公共点;
x=-
,y=
,
即P(-
,
)
(3)①PA=PB,理由如下:
y=kx+b当x=0时,y=b,即A(0,b);
当y=0时,x=-
,即B(-
,0),
P(-
,
),
PA=
,
PB=
,
∴PA=PB.
②P1A=P2B,理由如下:
y=kx+b当x=0时,y=b,即A(0,b);
当y=0时,x=-
,即B(-
,0),
联立l与C得
,
①-②,得
kx+b-
=0,
化简,得
kx2+bx-3=0,
解得P1(
,
)P2(
,
)
P1A2=(
)2+(
)2,P2B2=(
)2+(
)2,
∴P1A2=P2B2,
∴P1A=P2B.
|
①-②,得-x+2
| 3 |
| 3 |
| x |
化简,得x2-2
| 3 |
解得x1=x2=
| 3 |
| 3 |
直线l与双曲线C公共点的坐标为(
| 3 |
| 3 |
(2)证明:联立l与C得
|
①-②,得
kx+2
| -3k |
| 3 |
| x |
化简,得
kx2+2
| -3k |
a=k,b=2
| -3k |
△=b2-4ac=(2
| -3k |
∴kx2+2
| -3k |
x=-
| ||
| k |
| -3k |
即P(-
| ||
| k |
| -3k |
(3)①PA=PB,理由如下:
y=kx+b当x=0时,y=b,即A(0,b);
当y=0时,x=-
| b |
| k |
| b |
| k |
P(-
| ||
| k |
| -3k |
PA=
(
|
PB=
(
|
∴PA=PB.
②P1A=P2B,理由如下:
y=kx+b当x=0时,y=b,即A(0,b);
当y=0时,x=-
| b |
| k |
| b |
| k |
联立l与C得
|
①-②,得
kx+b-
| 3 |
| x |
化简,得
kx2+bx-3=0,
解得P1(
-b+
| ||
| 2k |
b+
| ||
| 2 |
-b-
| ||
| 2k |
b-
| ||
| 2 |
P1A2=(
-b+
| ||
| 2k |
-b+
| ||
| 2 |
b-
| ||
| 2k |
b-
| ||
| 2 |
∴P1A2=P2B2,
∴P1A=P2B.
点评:本题考查了反比例函数综合题,(1)利用了代入消元法解方程组;(2)利用了一元二次方程的根的判别式;(3)利用了函数与自变量的关系,两点间距离公式.

练习册系列答案
相关题目
 作图并解析:
作图并解析: 如图所示,在长为a厘米、宽为
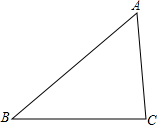
如图所示,在长为a厘米、宽为 如图,已知:BD=CE=AF,DE=DF=EF,△DEF为正三角形.求证:△ABC为正三角形.
如图,已知:BD=CE=AF,DE=DF=EF,△DEF为正三角形.求证:△ABC为正三角形.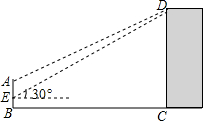 如图,某中学在主楼的顶部和大门的上方之间挂一些彩旗,经测量,得到大门的高度是5m,大门距主楼的距离是30m,在大门处测得主楼顶部的仰角是30°,而当时测倾器离地面1.4m.求:
如图,某中学在主楼的顶部和大门的上方之间挂一些彩旗,经测量,得到大门的高度是5m,大门距主楼的距离是30m,在大门处测得主楼顶部的仰角是30°,而当时测倾器离地面1.4m.求: 如图,在平面直角坐标系中,点A的坐标为(2,1).
如图,在平面直角坐标系中,点A的坐标为(2,1). 如图,分别以等腰直角三角形ACD的边AD,AC,CD为直径画半圆.
如图,分别以等腰直角三角形ACD的边AD,AC,CD为直径画半圆.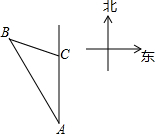 如图,某轮船沿正北方向航行,在点A处测得灯塔B在北偏西30°方向上,轮船以每小时25海里的速度航行2小时到达C后,测得灯塔B在北偏西75°方向上,问轮船到达灯塔B的正东方向时,轮船距灯塔有多远?(结果精确到0.1海里,参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.13,
如图,某轮船沿正北方向航行,在点A处测得灯塔B在北偏西30°方向上,轮船以每小时25海里的速度航行2小时到达C后,测得灯塔B在北偏西75°方向上,问轮船到达灯塔B的正东方向时,轮船距灯塔有多远?(结果精确到0.1海里,参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.13,