题目内容
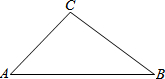 如图,在△ABC中,∠A=45°,AC=
如图,在△ABC中,∠A=45°,AC=| 2 |
| 3 |
(1)求S△ABC;
(2)求BC的长.
考点:勾股定理
专题:
分析:(1)过点C作CD⊥AB于点D,直接利用锐角三角函数关系得出DC的长,即可得出答案;
(2)首先求出BD的长,再利用勾股定理得出BC的长即可.
(2)首先求出BD的长,再利用勾股定理得出BC的长即可.
解答: 解:(1)过点C作CD⊥AB于点D,
解:(1)过点C作CD⊥AB于点D,
∵∠A=45°,AC=
,
∴AD=DC=ACsin45°=1,
∴S△ABC=
×1×(
+1)=
;
(2)∵AB=
+1,AD=CD=1,
∴BD=
,
∴BC=
=2.
 解:(1)过点C作CD⊥AB于点D,
解:(1)过点C作CD⊥AB于点D,∵∠A=45°,AC=
| 2 |
∴AD=DC=ACsin45°=1,
∴S△ABC=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
(2)∵AB=
| 3 |
∴BD=
| 3 |
∴BC=
| DB2+CD2 |
点评:此题主要考查了勾股定理以及三角形面积求法,得出AD,DC的长是解题关键.

练习册系列答案
相关题目
下列运算结果是负数的是( )
| A、(-5)+(-5) |
| B、(-5)-(-5) |
| C、(-5)*(-5) |
| D、(-5)÷(-5) |
 如图所示,在长为a厘米、宽为
如图所示,在长为a厘米、宽为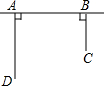 如图,铁路上A、B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C、D两村到E站的距离相等.
如图,铁路上A、B两点相距25km,C、D为两村庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,CB=10km,现在要在铁路AB上建一个土特产品收购站E,使得C、D两村到E站的距离相等. 如图,已知:BD=CE=AF,DE=DF=EF,△DEF为正三角形.求证:△ABC为正三角形.
如图,已知:BD=CE=AF,DE=DF=EF,△DEF为正三角形.求证:△ABC为正三角形.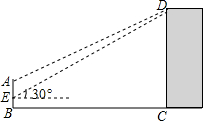 如图,某中学在主楼的顶部和大门的上方之间挂一些彩旗,经测量,得到大门的高度是5m,大门距主楼的距离是30m,在大门处测得主楼顶部的仰角是30°,而当时测倾器离地面1.4m.求:
如图,某中学在主楼的顶部和大门的上方之间挂一些彩旗,经测量,得到大门的高度是5m,大门距主楼的距离是30m,在大门处测得主楼顶部的仰角是30°,而当时测倾器离地面1.4m.求: 如图,分别以等腰直角三角形ACD的边AD,AC,CD为直径画半圆.
如图,分别以等腰直角三角形ACD的边AD,AC,CD为直径画半圆.