题目内容
甲骑摩托车,乙骑自行车从相距25km的两地相向而行.
(1)甲、乙同时出发经过0.5小时相遇,且甲每小时行驶路程是乙每小时行驶路程的3倍少6km,求乙骑自行车的速度.
(2)在甲骑摩托车和乙骑自行车与(1)相同的前提下,若乙先出发0.5小时,甲才出发,问:甲出发几小时后两人相遇?
(1)甲、乙同时出发经过0.5小时相遇,且甲每小时行驶路程是乙每小时行驶路程的3倍少6km,求乙骑自行车的速度.
(2)在甲骑摩托车和乙骑自行车与(1)相同的前提下,若乙先出发0.5小时,甲才出发,问:甲出发几小时后两人相遇?
考点:一元一次方程的应用
专题:
分析:(1)设乙骑自行车的速度为x千米/时,则甲的速度为(3x-6)千米/时,根据相遇问题路程的数量关系建立方程求出其解即可;
(2)设甲出发y小时后两人相遇,根据相遇问题路程的数量关系建立方程求出其解即可.
(2)设甲出发y小时后两人相遇,根据相遇问题路程的数量关系建立方程求出其解即可.
解答:解:(1)设乙骑自行车的速度为x千米/时,则甲的速度为(3x-6)千米/时,依题意有
0.5x+0.5(3x-6)=25,
解得x=14.
答:乙骑自行车的速度为14千米/时;
(2)3x-6=42-6=36,
设甲出发y小时后两人相遇,依题意有
0.5×14+(14+36)y=25,
解得y=0.36.
答:甲出发0.36小时后两人相遇.
0.5x+0.5(3x-6)=25,
解得x=14.
答:乙骑自行车的速度为14千米/时;
(2)3x-6=42-6=36,
设甲出发y小时后两人相遇,依题意有
0.5×14+(14+36)y=25,
解得y=0.36.
答:甲出发0.36小时后两人相遇.
点评:本题考查了列一元一次方程解实际问题的运用,相遇问题的数量关系的运用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
等腰三角形的一个角是80°,则它的顶角的度数是( )
| A、30° |
| B、80°或20° |
| C、80°或50° |
| D、20° |
如果3m表示向北走3m,那么-2m与6m分别表示( )
| A、向北走2m,向南走6m |
| B、向北走2m,向北走6m |
| C、向南走2m,向南走6m |
| D、向南走2m,向北走6m |
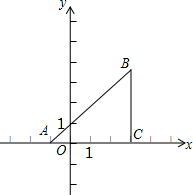 如图,已知直角坐标平面上的△ABC,AC=CB,∠ACB=90°,且A(-1,0),B(m,n),C(3,0).若抛物线y=ax2+bx-3经过A、C两点.
如图,已知直角坐标平面上的△ABC,AC=CB,∠ACB=90°,且A(-1,0),B(m,n),C(3,0).若抛物线y=ax2+bx-3经过A、C两点. 已知关于x的方程x2-kx+k-1=0.
已知关于x的方程x2-kx+k-1=0.