题目内容
6. 如图,已知等腰直角△ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时点A与点M重合,让△ABC沿着MN方向以每秒1cm的速度移动,最后点A与点N重合.
如图,已知等腰直角△ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时点A与点M重合,让△ABC沿着MN方向以每秒1cm的速度移动,最后点A与点N重合.(1)直接写出重叠部分周长y(cm)与运动时间x(秒)之间的函数关系式及自变量x的取值范围;
(2)当运动时间为多少秒时,重叠部分周长等于△ABC周长的一半.(结果精确到1秒)
分析 (1)根据题意可知重叠部分为等腰直角三角形,利用勾股定理可求得斜边长,最后求得周长与x之间的函数关系式即可;
(2)先证明△ABC∽△ADM,然后利用相似三角形的相似比等于周长比求解即可..
解答 解:(1)如图所示: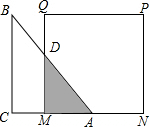
∵△ABC为等腰直角三角形,
∴∠BAC=45°.
又∵∠DMA=90°,
∴∠MDA=∠DAM=45°
∴AM=DM=x.
由勾股定理得:DA=$\sqrt{M{D}^{2}+M{A}^{2}}$=$\sqrt{2}$x,
∴y=2x+$\sqrt{2}$x(0≤x≤10).
(2)∵∠DMA=∠C,∠A=∠A,
∴△ABC∽△ADM.
∵重叠部分周长等于△ABC周长的一半,
∴$\frac{AM}{AC}=\frac{1}{2}$,即$\frac{AM}{10}=\frac{1}{2}$.
解得:AM=5.
∴运动时间为5秒时,重叠部分周长等于△ABC周长的一半.
点评 本题主要考查的是动点问题的函数图形,确定出三角形DMA为等腰直角三角形是解题的关键.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
 如图所示,∠BAC=85°,BF平分∠ABC交AC于点F,∠BFC=100°,求∠C的度数.
如图所示,∠BAC=85°,BF平分∠ABC交AC于点F,∠BFC=100°,求∠C的度数.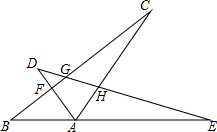 如图,在△ABC中,∠BAC=120°,将△ABC绕点A顺时针旋转60°得△ADE,则图中有3对全等三角形,它们是△ADE≌△ABC,BAF≌△DAH,△AEH≌△ACF.
如图,在△ABC中,∠BAC=120°,将△ABC绕点A顺时针旋转60°得△ADE,则图中有3对全等三角形,它们是△ADE≌△ABC,BAF≌△DAH,△AEH≌△ACF. 如图,四边形ABCD中,AD∥BC,BA,CD的延长线相交于点E,若AD=2,BC=3,BA=2.5,则AE=5,理由是:相似三角形的性质.
如图,四边形ABCD中,AD∥BC,BA,CD的延长线相交于点E,若AD=2,BC=3,BA=2.5,则AE=5,理由是:相似三角形的性质.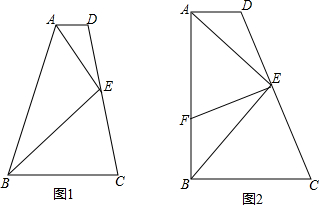
 现有一块边长为a的正方形草坪,如图所示,将其相邻两边均扩大b,用两种方法计算扩大后草坪的面积.由此验证我们所学过的一个非常熟悉的公式,并写出这个公式.
现有一块边长为a的正方形草坪,如图所示,将其相邻两边均扩大b,用两种方法计算扩大后草坪的面积.由此验证我们所学过的一个非常熟悉的公式,并写出这个公式. 如图,把Rt△ABC的斜边放在直线l上,按顺时针方向在l上转动两次,使它转到△A″B″C″的位置,设BC=1,AC=$\sqrt{3}$,求当顶点A运动到A″位置时,点A经过的路径长度.
如图,把Rt△ABC的斜边放在直线l上,按顺时针方向在l上转动两次,使它转到△A″B″C″的位置,设BC=1,AC=$\sqrt{3}$,求当顶点A运动到A″位置时,点A经过的路径长度.