题目内容
15. 如图,把Rt△ABC的斜边放在直线l上,按顺时针方向在l上转动两次,使它转到△A″B″C″的位置,设BC=1,AC=$\sqrt{3}$,求当顶点A运动到A″位置时,点A经过的路径长度.
如图,把Rt△ABC的斜边放在直线l上,按顺时针方向在l上转动两次,使它转到△A″B″C″的位置,设BC=1,AC=$\sqrt{3}$,求当顶点A运动到A″位置时,点A经过的路径长度.
分析 首先利用三角形函数求得∠ABC的度数,则旋转角即可求得,然后利用弧长公式即可求解.
解答 解:∵直角△ABC中,tan∠ABC=$\frac{AC}{BC}$=$\sqrt{3}$,
∴∠ABC=60°,
则∠ABA'=120°,AB=2BC=2,
即$\widehat{AA'}$的长是$\frac{120π×2}{180}$=$\frac{4π}{3}$,
$\widehat{A'A''}$的长是$\frac{90•π•\sqrt{3}}{180}$=$\frac{\sqrt{3}}{2}$π.
则点A经过的路径长是$\frac{4π}{3}$+$\frac{\sqrt{3}}{2}$π=$\frac{8+3\sqrt{3}}{6}$π.
点评 本题考查了三角函数以及弧长计算公式,正确确定旋转角的度数是关键.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
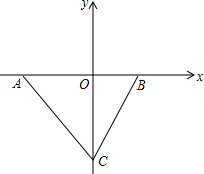 如图,在平面直角坐标系中,点D在y轴上,点C的坐标为(0,-4),直线AD平分∠BAC,线段OA、OB的长满足一元二次方程x2-5x+6=0的两根(OA>OB).
如图,在平面直角坐标系中,点D在y轴上,点C的坐标为(0,-4),直线AD平分∠BAC,线段OA、OB的长满足一元二次方程x2-5x+6=0的两根(OA>OB). 如图,已知等腰直角△ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时点A与点M重合,让△ABC沿着MN方向以每秒1cm的速度移动,最后点A与点N重合.
如图,已知等腰直角△ABC的直角边长与正方形MNPQ的边长均为10cm,AC与MN在同一直线上,开始时点A与点M重合,让△ABC沿着MN方向以每秒1cm的速度移动,最后点A与点N重合.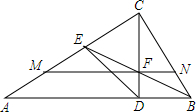 如图,在△ABC中,∠C=90°,CD⊥AB于D,BE为∠ABC的角平分线,BE交CD于点F,M为线段AC上一点,且AM=EC,直线MF与CB交于点N.求证:DE⊥DN.
如图,在△ABC中,∠C=90°,CD⊥AB于D,BE为∠ABC的角平分线,BE交CD于点F,M为线段AC上一点,且AM=EC,直线MF与CB交于点N.求证:DE⊥DN.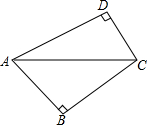 如图,四边形ABCD的一组对角∠ABC、∠ADC都是直角.
如图,四边形ABCD的一组对角∠ABC、∠ADC都是直角. 如图,四边形ABCD中,∠B=∠D=90°,点E为AC的中点,则A,B,C,D四点共圆吗?
如图,四边形ABCD中,∠B=∠D=90°,点E为AC的中点,则A,B,C,D四点共圆吗? 如图是长春节某花园的平面图,花园长为100米,宽为50米,在它的四角各建有一个同样大小的正方形观光休息亭,四周建有与观光休息亭等宽的观光大道,其余部分(图中阴影部分)种植的是不同花草.若设观光休息亭的边长为a米,求种植花草部分的面积.
如图是长春节某花园的平面图,花园长为100米,宽为50米,在它的四角各建有一个同样大小的正方形观光休息亭,四周建有与观光休息亭等宽的观光大道,其余部分(图中阴影部分)种植的是不同花草.若设观光休息亭的边长为a米,求种植花草部分的面积. 已知:△ABC中,ED∥BC,BD与CE交于点O,连接AO并延长交BC于点M,求证:M是BC中点.
已知:△ABC中,ED∥BC,BD与CE交于点O,连接AO并延长交BC于点M,求证:M是BC中点.