题目内容
如图，已知∠A=∠D=90°，E、F在线段BC上，DE与AF交于点O，且AB=CD，BE=CF．求证：Rt△ABF≌Rt△DCE．
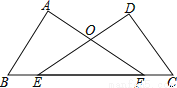
证明见解析.
【解析】由于△ABF与△DCE是直角三角形，根据直角三角形全等的判定的方法即可证明．
证明：∵BE=CF，
∴BE+EF=CF+EF，即BF=CE，
∵∠A=∠D=90°，
∴△ABF与△DCE都为直角三角形，
在Rt△ABF和Rt△DCE中，
BC=CE，AB=CD，
∴Rt△ABF≌Rt△DCE（HL）．
练习册系列答案
相关题目
如图，在△ABC中，已知∠C＝90°，AC=4，BC=3，那么下列结论不正确的是（ ）
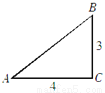
A. sinA=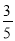
B. cosA=
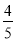C. tanA=
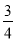D. cosB=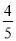
D
【解析】∵∠C＝90°，AC=4，BC=3，∴AB==5，
∴sinA==，cosA== ， tanA== ， cosB==，
故选D. 分解因式：6x－4xy
2x(3－2y)
【解析】试题分析：根据提公因式法分解因式，先确定公因式2x，再提取公因式即可.
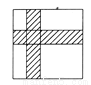
试题解析：6x-4xy=2x（3-2y）. 如图所示，一张白色正方形纸片的边长是10 cm，被两张宽为2 cm的阴影纸条分为四个白色的长方形部分，请你利用平移的知识求出图中白色部分的面积．
64 cm2
【解析】试题分析：将横向的小路平移至正方形的上边，将纵向小路平移至正方形的左边，则剩余部分即为白色部分的面积．
【解析】
将横向的小路平移至正方形的上边，将纵向小路平移至正方形的左边，
所以白色部分的面积＝(10－2)(10－2)＝64cm2． 下列说法正确的是 ( )
A. 两个全等的图形可看做其中一个是由另一个平移得到的
B. 由平移得到的两个图形对应点连线互相平行(或共线)
C. 由平移得到的两个等腰三角形周长一定相等，但面积未必相等
D. 边长相等的两个正方形一定可以通过平移得到
B
【解析】试题分析：A、全等三角形仅仅是反映了两个三角形的形状和大小关系，而平移既需要两个三角形全等，还需要两个三角形有一种特殊的位置关系，故错误；
B、符合平移的性质，故正确；
C、由平移得到的两个等腰三角形全等，面积必相等，故错误；
D、平移还需要具备一种特殊的位置关系，故错误．
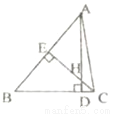
故选B． 如图，△ABC中，AD⊥BC，CE⊥AB，垂足分别为D、E，AD、CE交于点H，请你添加一个适当的条件：_____________，使△AEH≌△CEB．
AH＝BC或EA＝EC或EH＝EB等；
【解析】∵AD⊥BC，CE⊥AB，垂足分别为D、E，
∴∠BEC=∠AEC=90°，
在Rt△AEH中，∠EAH=90°﹣∠AHE，
又∵∠EAH=∠BAD，
∴∠BAD=90°﹣∠AHE，
在Rt△AEH和Rt△CDH中，∠CHD=∠AHE，
∴∠EAH=∠DCH，
∴∠EAH=90°﹣∠CHD=∠BCE，
... 在直角三角形中，其中一个锐角是另一个锐角的2倍，则此三角形中最小的角是（ ）
A. 15° B. 30° C. 60° D. 90°
B
【解析】【解析】
设较小的锐角是x°，则另一个锐角是2x°．
由题意得：x+2x=90，解得x=30．
即此三角形中最小的角是30°．
故选B． 如图，在□ABCD中，已知AD=8cm，AB=6cm，DE平分∠ADC交BC边于点E，则BE等于（ ）
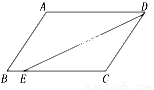
A. 2cm B. 4cm C. 6cm D. 8cm
A
【解析】试题分析：由平行四边形对边平行根据两直线平行，内错角相等可得∠EDA=∠DEC，而DE平分∠ADC，进一步推出∠EDC=∠DEC，在同一三角形中，根据等角对等边得CE=CD=6，则BE可求BE=BC-EC=8-6=2．
故选：A． 如果关于x的不等式（a－1）x＞a－1的解集为x＜1，那么a的取值范围是（ ）
A. a≤1 B. a≥1 C. a＜1 D. a＜0
C
【解析】由含有a的不等式（a-1）x＞a-1的解集为：x＜1，根据不等式的基本性质3，可知a-1＜0，解得a＜1.
故选：C.