题目内容
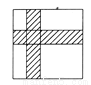
如图所示，一张白色正方形纸片的边长是10 cm，被两张宽为2 cm的阴影纸条分为四个白色的长方形部分，请你利用平移的知识求出图中白色部分的面积．
64 cm2
【解析】试题分析：将横向的小路平移至正方形的上边，将纵向小路平移至正方形的左边，则剩余部分即为白色部分的面积．
【解析】
将横向的小路平移至正方形的上边，将纵向小路平移至正方形的左边，
所以白色部分的面积＝(10－2)(10－2)＝64cm2．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
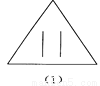
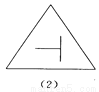
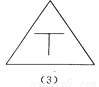
如图所示的四个图形中，从几何图形变换的角度考虑，哪一个与其他三个不同?请指出这个图形，并简述你的理由．
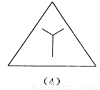
图(2)，仅它不是轴对称图形
【解析】试题分析：观察图形发现（1）（3）（4）都是轴对称图形，而（2）不是轴对称图形，由此即可得出结论．
试题解析：【解析】
（1）（3）（4）都是轴对称图形，而（2）不是轴对称图形．故从几何图形变换的角度考虑，图（2）与其它三个不同． 如图，某地修建高速公路，要从B地向C地修一座隧道(B、C在同一水平面上)，为了测量B、C两地之间的距离，某工程师乘坐热气球从C地出发，垂直上升100m到达A处，在A处观察B地的俯角为30°，则B、C两地之间的距离为( )
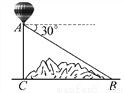
A. 100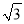
m B. 50
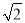m C. 50
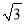m D. 
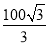m
A
【解析】试题分析：根据题意得：∠ABC=30°，AC⊥BC，AC=100m，
在Rt△ABC中，BC=（m）．
故选A． －9a2b＋3ac2－6abc各项的公因式是_______；
－3a
【解析】根据提公因式法因式分解，可知其是首项为“﹣”的多项式，因此可知其公因式为-3a.
故答案为：-3a. 菱形以特殊的对称美而深受人们的喜爱，在生产生活中有着广泛的应用，小龙家里有一面长4.2m、宽2.8m的墙壁准备装修，现有如图甲所示的型号瓷砖，其形状是一块长30cm、宽20cm的矩形，中间白色部分为菱形，阴影部分为带淡蓝色花纹的全等的四个直角三角形，解答下列各问：
（1）小龙家里的墙壁最少要贴这种瓷砖多少块？
（2）全部贴满后，这面墙壁上有多少个有淡蓝色花纹的菱形？
(1)196;(2)169
【解析】试题分析：（1）根据墙壁的长与宽以及矩形瓷砖的长与宽进行计算求出所需要贴的瓷砖的行数与列数，然后进行计算即可得解；
（2）根据（1）中结论即可求出淡蓝色花纹的菱形个数．
试题解析：
【解析】
（1）4.2m＝420cm，2.8m＝280cm，
∵420÷30＝14，280÷20＝14，
∴贴满墙壁需要14行14列瓷砖，
... 一个三角形最初的一个顶点为A，把它先向下平移4个单位长度时的位置记为B，再向左平移3个单位长度时的位置记为C，则由A，B，C三点所组成的三角形的周长为 ( )
A. 7 B. 14 C. 12 D. 15
C
【解析】试题分析：如图所示：
AB＝4，BC＝3，
则AC＝5，
故由A，B，C三点所组成的三角形的周长为：3＋4＋5＝12．
故选C． 如图，已知∠A=∠D=90°，E、F在线段BC上，DE与AF交于点O，且AB=CD，BE=CF．求证：Rt△ABF≌Rt△DCE．
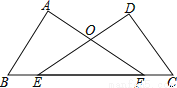
证明见解析.
【解析】由于△ABF与△DCE是直角三角形，根据直角三角形全等的判定的方法即可证明．
证明：∵BE=CF，
∴BE+EF=CF+EF，即BF=CE，
∵∠A=∠D=90°，
∴△ABF与△DCE都为直角三角形，
在Rt△ABF和Rt△DCE中，
BC=CE，AB=CD，
∴Rt△ABF≌Rt△DCE（HL）． 如图，一个矩形纸片，剪去部分后得到一个三角形，则图中∠1+∠2的度数是（ ）
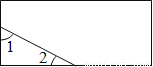
A. 30° B. 60° C. 90° D. 120°
C
【解析】试题分析：由题意得，剩下的三角形是直角三角形，
所以，∠1+∠2=90°．
故选C． 已知x=3是关于x的不等式3x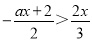
的解，求a的取值范围.
a＜4
【解析】试题分析：先根据不等式的解的定义，将x=3代入不等式3x，得到．
9，解此不等式，即可求出a的取值范围．
试题解析：∵x=3是关于x的不等式3x的解,
∴3×3.
整理 得3a＜12，
解得a＜4．
故a的取值范围是a＜4．