��Ŀ����
16���Ķ����в��ϣ�ͨ��Сѧ��ѧϰ����֪���������ɷ�Ϊ����������͡��ٷ����������ٷ������ɻ�Ϊ���������磺$\frac{8}{3}$=$\frac{6+2}{3}$=2+$\frac{2}{3}$=2$\frac{2}{3}$
���Ƕ��壺�ڷ�ʽ�У�����ֻ����һ����ĸ�ķ�ʽ�������ӵĴ������ڻ���ڷ�ĸ�Ĵ���ʱ�����dz�֮Ϊ���ٷ�ʽ���������ӵĴ���С�ڷ�ĸ�Ĵ���ʱ�����dz�֮Ϊ�����ʽ����
��$\frac{x-1}{x+1}$��$\frac{{x}^{2}}{x-1}$�����ķ�ʽ���Ǽٷ�ʽ�����磺$\frac{3}{x+1}$��$\frac{2x}{{x}^{2}+1}$�����ķ�ʽ�������ʽ�����Ƶģ��ٷ�ʽҲ���Ի�Ϊ����ʽ��������ʽ�����ʽ�ĺ͵���ʽ����
�磺$\frac{x-1}{x+1}=\frac{��x+1��-2}{x+1}=1-\frac{2}{x+1}$��
���磺$\frac{{x}^{2}}{x-1}=\frac{{x}^{2}-1+1}{x-1}=\frac{��x+1����x-1��+1}{x-1}$=x+1+$\frac{1}{x-1}$
����������⣺
��1����ʽ$\frac{2}{x}$�����ʽ����桱�١�����
��2�����ٷ�ʽ$\frac{x-1}{x+2}$��Ϊ����ʽ����ʽΪ1-$\frac{3}{x+2}$��
��3���ѷ�ʽ$\frac{2x-1}{x+1}$��Ϊ����ʽ�����$\frac{2x-1}{x+1}$��ֵΪ��������x������ֵ��
���� ��1���������ʽ�Ķ��弴���жϣ�
��2����������ѷ�ʽ�ķ��ӻ���x+2����ʽ��Ȼ������ͬ��ĸ�ķ�ʽ�ļӷ�������⣻
��3����ʽ$\frac{2x-1}{x+1}$��Ϊ����ʽ���ѷ��ӻ���2��x+1��-3����ʽ��Ȼ������ͬ��ĸ�ķ�ʽ�ļӷ����ɴ���ʽ��
$\frac{2x-1}{x+1}$��ֵΪ��������$\frac{3}{x+1}$��ֵһ������������x+1һ����3��Լ�����Ӷ����x��ֵ��
��� �⣺��1��$\frac{2}{x}$�����ʽ���ʴ��ǣ��棻
��2��$\frac{x-1}{x+2}$=$\frac{x+2-3}{x+2}$=1-$\frac{3}{x+2}$��
�ʴ��ǣ�1-$\frac{3}{x+2}$��
��3��$\frac{2x-1}{x+1}$=$\frac{2x+2-3}{x+1}$=$\frac{2��x+1��-3}{x+1}$=2-$\frac{3}{x+1}$��
��$\frac{2x-1}{x+1}$��ֵΪ��������xΪ������
��x+1Ϊ3��Լ����
��x+1��ֵΪ1��-1��3��-3��
��x��ֵΪ0��-2��2��-4��
���� ���⿼���˷�ʽ�Ļ�����㣬��ȷ�Է�ʽ�ķ�ĸ���б��Σ�����ͬ��ĸ�ķ�ʽ�ļӷ������ǹؼ���

��ϰ��ϵ�д�
�����Ŀ
 ��ͼ����ƽ��ֱ������ϵ�У���֪��A��2��0����P�Ǻ���y=x��x��0��ͼ����һ�㣬PQ��AP��y���ڵ�Q�����P�ĺ�����Ϊa����Q��������Ϊb����OP��10$\sqrt{2}$����b��ȡֵ��Χ��
��ͼ����ƽ��ֱ������ϵ�У���֪��A��2��0����P�Ǻ���y=x��x��0��ͼ����һ�㣬PQ��AP��y���ڵ�Q�����P�ĺ�����Ϊa����Q��������Ϊb����OP��10$\sqrt{2}$����b��ȡֵ��Χ��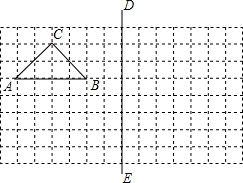 ��ͼ������������ͼ��ÿС���Ϊ�߳���1�������Σ���������и��⣺
��ͼ������������ͼ��ÿС���Ϊ�߳���1�������Σ���������и��⣺ ��ͼ������ABCD�У�AB=4��BC=6���Խ���AC��BD���ڵ�O���ӳ�DC��E������OE����BC�ڵ�F����CE=2������CF�ij���
��ͼ������ABCD�У�AB=4��BC=6���Խ���AC��BD���ڵ�O���ӳ�DC��E������OE����BC�ڵ�F����CE=2������CF�ij���
 ��ͼ����x����������A��-3��0����B��3��0������һ����C���߶�AB�ϴӵ�A�˶�����B������A��B�غϣ����ֱ���AC��BCΪ�ױ���������AEC�͵�����BFC������E��Fǡ�����ڷ���������y=-$\frac{5}{x}$��x��0����y=$\frac{2}{x}$��x��0����ͼ���ϣ�����EF���������˶������У��߶�EF���ȵı仯����ǣ�������
��ͼ����x����������A��-3��0����B��3��0������һ����C���߶�AB�ϴӵ�A�˶�����B������A��B�غϣ����ֱ���AC��BCΪ�ױ���������AEC�͵�����BFC������E��Fǡ�����ڷ���������y=-$\frac{5}{x}$��x��0����y=$\frac{2}{x}$��x��0����ͼ���ϣ�����EF���������˶������У��߶�EF���ȵı仯����ǣ�������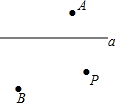 ��ͼ��ƽ������ֱ��a��ֱ��a�������A��B��P��
��ͼ��ƽ������ֱ��a��ֱ��a�������A��B��P��