题目内容
8. (1)解不等式组:$\left\{\begin{array}{l}{2x-1>x+1}\\{x+8>4x-1}\end{array}\right.$,并把解集在数轴上表示出来.
(1)解不等式组:$\left\{\begin{array}{l}{2x-1>x+1}\\{x+8>4x-1}\end{array}\right.$,并把解集在数轴上表示出来.(2)先化简,再求值:($\frac{x}{x-1}$-$\frac{1}{{x}^{2}-x}$)÷(x+1),其中x=$\sqrt{2}$.
分析 (1)先解不等式组中的每一个不等式,得到不等式组的解集,再把不等式的解集表示在数轴上即可.
(2)先根据分式混合运算的法则把原式进行化简,再根据x是方程x2-2x=0的根求出x的值,把x的值代入进行计算即可.
解答 解:(1)由$\left\{\begin{array}{l}{2x-1>x+1}\\{x+8>4x-1}\end{array}\right.$,得
$\left\{\begin{array}{l}{x>2}\\{x<3}\end{array}\right.$,
所以原不等式组的解集是2<x<3,表示在数轴上是: ;
;
(2)($\frac{x}{x-1}$-$\frac{1}{{x}^{2}-x}$)÷(x+1),
=$\frac{(x-1)(x+1)}{x(x-1)}$×$\frac{1}{x+1}$,
=$\frac{1}{x}$.
把x=$\sqrt{2}$代入,得
原式=$\frac{1}{\sqrt{2}}$=$\frac{\sqrt{2}}{2}$.
点评 本题考查的是分式的化简求值,解一元一次不等式组以及在数轴上表示不等式的解集.解不等式时,学会移项,左边的移到右边,右边的移到左边.所移的项正负号互换;把字母移归到一边,常数移归到另一边.中间的大于、小于号尽量不要动,不然易出错.(两边同除以负数时,大于、小于号调头).

练习册系列答案
相关题目
19. 如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=35°,那么∠2是( )°.
如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=35°,那么∠2是( )°.
 如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=35°,那么∠2是( )°.
如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=35°,那么∠2是( )°.| A. | 55 | B. | 35 | C. | 65 | D. | 25 |
16.根据等式的性质,下列变形正确的是( )
| A. | 若2x=a,则x=2a | B. | 若$\frac{x}{2}$+$\frac{x}{3}$=1,则3x+2x=1 | ||
| C. | 若ab=bc,则a=c | D. | 若$\frac{a}{c}$=$\frac{b}{c}$,则a=b |
13.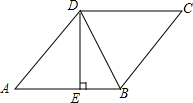 如图,在菱形ABCD中,DE⊥AB,cosA=$\frac{3}{5}$,BE=2,则tan∠DBE的值是( )
如图,在菱形ABCD中,DE⊥AB,cosA=$\frac{3}{5}$,BE=2,则tan∠DBE的值是( )
 如图,在菱形ABCD中,DE⊥AB,cosA=$\frac{3}{5}$,BE=2,则tan∠DBE的值是( )
如图,在菱形ABCD中,DE⊥AB,cosA=$\frac{3}{5}$,BE=2,则tan∠DBE的值是( )| A. | $\frac{1}{2}$ | B. | 2 | C. | 10$\sqrt{3}$ | D. | $\frac{\sqrt{5}}{5}$ |
20. 如图所示几何体的俯视图是( )
如图所示几何体的俯视图是( )
 如图所示几何体的俯视图是( )
如图所示几何体的俯视图是( )| A. |  | B. |  | C. |  | D. |  |