Question

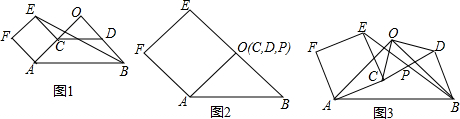
3．问题背景：△AOB、△COD是两个等腰直角三角形，现将直角顶点以及两直角边都重合在一起，如图1所示，点P是CD中点，连接BP并延长到E使PE=BP，连接EC，作平行四边形ACEF，小林针对平行四边形ACEF形状进行了如下探究：
观察操作：（1）小林先假设小等腰直角三角形的直角边非常小，这时三角形可以看作一个点，如图2所示，并提出猜想四边形ACEF是正方形；
猜想证明：（2）小林对比图1和图2的情形，完成了（1）中的猜想，请借助图1帮他证明这个猜想．
拓展延伸：（3）如图3所示，现将等腰直角三角形COD绕点O逆时针旋转一定角度，其它条件都不改变，原来结论是否仍然成立？请说明理由．

Answer 1

分析 （1）根据已知直接证明有一个直角且邻边相等即可；
（2）通过证明三角形CEP和三角形DBP全等，结合等量代换即可证明；
（3）与（2）同理可证EC=DB，EC∥DB，进一步证明△AOC≌△BOD，结合等量代换和平行线的性质即可解答．

解答 解：（1）正方形；
如图2，

∵△AOB是等腰直角三角形，
∴∠AOE=90°，AO=BO，
∵OE=BO，
∴AO=OE，
∴平行四边形ACEF是正方形；
（2）如图1，

∵P是CD的中点，
∴PC=PD，
在△CPE和△BPD中，
$\left\{\begin{array}{l}{PC=PE}\\{∠CPE=∠DPB}\\{PE=PB}\end{array}\right.$，
∴△CPE≌△BPD，
∴EC=DB，
∵OA=OB，OC=OD，
∴AC=DB，
∴EC=AC，
∴平行四边形ACEF是菱形，
∵△CPE≌△BPD，
∴∠CEP=∠DBP，
∴EC∥OB，
∵∠O=90°，
∴∠ACE=90°，
∴菱形ACEF是正方形；
（3）如图3，

与（2）同理可证△CPE≌△BPD，
∴EC=DB，EC∥DB，
∵∠AOC+∠COB=∠COB+∠DOB=90°，
∴∠AOC=∠DOB，
在△AOC和△BOD中，
$\left\{\begin{array}{l}{OA=OB}\\{∠AOC=∠BOD}\\{OC=OD}\end{array}\right.$，
∴△AOC≌△BOD，
∵∠COD=90°，
∴△AOC可以看作△BOD顺时针绕点O旋转90°得到，
∴AC⊥DB，AC=DB，
∴EC=AC，
∴平行四边形ACEF是菱形，
∵EC∥DB，
∴AC⊥EC，
∴菱形ACEF是正方形．

点评 此题主要考查几何变换中的旋转，在旋转中找到并证明全等三角形，并灵活运用全等三角形的性质进行推理是解题的关键．