题目内容
15.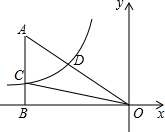 如图,已知双曲线y=-$\frac{3}{x}$(x<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C,则△AOC的面积为( )
如图,已知双曲线y=-$\frac{3}{x}$(x<0)经过直角三角形OAB斜边OA的中点D,且与直角边AB相交于点C,则△AOC的面积为( )| A. | 6 | B. | $\frac{9}{2}$ | C. | 3 | D. | 2 |
分析 设出点D的坐标,由点D为线段AO的中点可表示出点A的坐标,再利用分割图形法求三角形的面积结合三角形的面积公式以及反比例函数系数k的几何意义即可得出结论.
解答 解:设点D的坐标为(-m,$\frac{3}{m}$)(m>0),则点A的坐标为(-2m,$\frac{6}{m}$).
S△AOC=S△ABO-S△BOC=$\frac{1}{2}$×2m×$\frac{6}{m}$-$\frac{1}{2}$×|-3|=$\frac{9}{2}$.
故选B.
点评 本题考查了反比例函数图象上点的坐标特征、反比例函数系数k的几何意义以及三角形的面积公式,解题的关键是利用分割图形法求三角形的面积.本题属于基础题,难度不大,解决该题型题目时,找出点的坐标,再结合反比例函数系数k的几何意义求出图形的面积是关键.

练习册系列答案
相关题目
5.如果单项式2anb2c是六次单项式,那么n=( )
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
6.方程2x2-6x+3=0的根的情况是( )
| A. | 有两个同号的不相等的实数根 | B. | 有两个异号的不相等的实数根 | ||
| C. | 有两个相等的实数根 | D. | 没有实数根 |
3.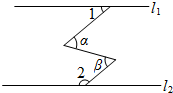 如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=( )
如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=( )
 如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=( )
如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=( )| A. | 100° | B. | 120° | C. | 140° | D. | 160° |
10.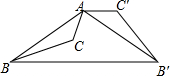 如图,已知钝角三角形ABC,将△ABC绕点A按逆时针方向旋转110°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( )
如图,已知钝角三角形ABC,将△ABC绕点A按逆时针方向旋转110°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( )
 如图,已知钝角三角形ABC,将△ABC绕点A按逆时针方向旋转110°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( )
如图,已知钝角三角形ABC,将△ABC绕点A按逆时针方向旋转110°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( )| A. | 55° | B. | 65° | C. | 75° | D. | 85° |
16.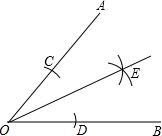 观察图中尺规作图痕迹,下列说法错误的是( )
观察图中尺规作图痕迹,下列说法错误的是( )
 观察图中尺规作图痕迹,下列说法错误的是( )
观察图中尺规作图痕迹,下列说法错误的是( )| A. | OE是∠AOB的平分线 | B. | OC=OD | ||
| C. | 点C、D到OE的距离不相等 | D. | ∠AOE=∠BOE |
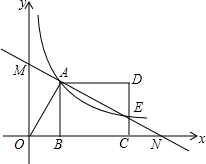 如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=$\frac{3}{2}$.
如图,反比例函数y=$\frac{k}{x}$(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=$\frac{3}{2}$.
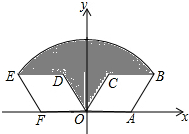 如图,菱形OABC的顶点A的坐标为(2,0),∠COA=60°,将菱形OABC绕坐标原点O逆时针旋转120°得到菱形ODEF,则图中阴影部分的面积为4π-2$\sqrt{3}$.
如图,菱形OABC的顶点A的坐标为(2,0),∠COA=60°,将菱形OABC绕坐标原点O逆时针旋转120°得到菱形ODEF,则图中阴影部分的面积为4π-2$\sqrt{3}$.