题目内容
16.下列关于x的方程中,没有实数解的是( )| A. | x2-4x+4=0 | B. | x2-2x-3=0 | C. | x2-2x=0 | D. | x2-2x+5=0 |
分析 分别计算出每个方程中的△的值,判断即可.
解答 解:A、△=(-4)2-4×1×4=0,方程有两个相等实数根;
B、△=(-2)2-4×1×(-3)=16>0,方程有两个不相等的实数根;
C、△=(-2)2-4×1×0=4>0,方程有两个不相等的实数根;
D、△=(-2)2-4×1×5=-16<0,方程没有实数根,
故选:D.
点评 本题主要考查一元二次方程根的判别式,一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:①当△>0时,方程有两个不相等的两个实数根;②当△=0时,方程有两个相等的两个实数根;③当△<0时,方程无实数根.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
4.不等式组$\left\{\begin{array}{l}{2x-1<1}\\{-x≤2}\end{array}\right.$的解集为( )
| A. | -2<x<1 | B. | x<1 | C. | -2≤x<1 | D. | x≥-2 |
11.借助计算器可求得$\sqrt{{4^2}+{3^2}}=5,\sqrt{{{44}^2}+{{33}^2}}=55,\sqrt{{{444}^2}+{{333}^2}}$=555,…,仔细观察上面几道题的计算结果,试猜想$\sqrt{{{\underbrace{44…4}_{2016个}}^2}+{{\underbrace{33…3}_{2016个}}^2}}$=( )
| A. | $\underbrace{55…5}_{2013个}$ | B. | $\underbrace{55…5}_{2014个}$ | C. | $\underbrace{55…5}_{2015个}$ | D. | $\underbrace{55…5}_{2016个}$ |
1.tan45°的值等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
5.如果单项式2anb2c是六次单项式,那么n=( )
| A. | 6 | B. | 5 | C. | 4 | D. | 3 |
6.方程2x2-6x+3=0的根的情况是( )
| A. | 有两个同号的不相等的实数根 | B. | 有两个异号的不相等的实数根 | ||
| C. | 有两个相等的实数根 | D. | 没有实数根 |
 如图是由四个小正方体搭成的一个几何体,这个几何体的俯视图是( )
如图是由四个小正方体搭成的一个几何体,这个几何体的俯视图是( )



 用5个完全相同的小正方体组成的如图的立体图形,它的左视图是( )
用5个完全相同的小正方体组成的如图的立体图形,它的左视图是( )



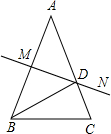 如图,在△ABC中,AB=AC=8,BC=5,∠A=40°,AB边的中垂线MN交AC于点D,交AB于点M.
如图,在△ABC中,AB=AC=8,BC=5,∠A=40°,AB边的中垂线MN交AC于点D,交AB于点M.