题目内容
5.已知第一个三角形的面积是1,它的三条中位线组成第1个三角形,第2个三角形的三条中位线又组成第3个三角形,以此类推…第2014个三角形的面积为( )| A. | $\frac{1}{{2}^{4022}}$ | B. | $\frac{1}{{2}^{4024}}$ | C. | $\frac{1}{{2}^{4026}}$ | D. | $\frac{1}{{2}^{4028}}$ |
分析 由A2,B2,C2分别是△A1B1C1各边的中点,根据三角形中位线的性质和有三组对应边的比相等的两个三角形相似得到△A2B2C2∽△A1B1C1,所以S△A2B2C2:S△A1B1C1=C2B22:C1B12=1:22,得到即S△A2B2C2=$\frac{1}{4}$,同理可得S△A3B3C3=$\frac{1}{4}$×$\frac{1}{4}$=($\frac{1}{4}$)2,以此类推即可得到第n个三角形的面积,据此进行计算即可.
解答 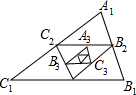 解:∵A2,B2,C2分别是△A1B1C1各边的中点,
解:∵A2,B2,C2分别是△A1B1C1各边的中点,
∴△A2B2C2∽△A1B1C1,
∴S△A2B2C2:S△A1B1C1=C2B22:C1B12=1:22,
即S△A2B2C2=$\frac{1}{4}$,
∴S△A3B3C3=$\frac{1}{4}$×$\frac{1}{4}$=($\frac{1}{4}$)2,
以此类推,第n个三角形的面积是($\frac{1}{4}$)n-1=($\frac{1}{2}$)2n-2,
∴第2014个三角形的面积为($\frac{1}{2}$)2×2014-2=$\frac{1}{{2}^{4026}}$.
故选:C.
点评 本题考查了三角形中位线定理以及三角形相似的性质的运用,解题的关键是找到问题的一般规律.

练习册系列答案
相关题目
13.下列判断正确的是( )
| A. | 0.560精确到0.01 | B. | 3.8万精确到0.1 | ||
| C. | 600精确到个位 | D. | 1.30×104精确到百分位 |
 如图,在边长为1的小正方形组成的网格中,△ABC的顶点均在格点上,请按要求完成下列各题:
如图,在边长为1的小正方形组成的网格中,△ABC的顶点均在格点上,请按要求完成下列各题: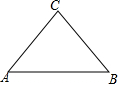 如图,
如图,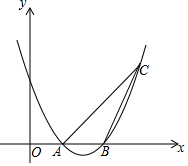 如图,抛物线y=x2-4x+3与x轴交于A,B两点,且过点C(4,3),在对称轴右侧的抛物线上是否存在点P,使∠PAC>∠ACB,若存在,求出点P的横坐标xP的取值范围;若不存在,请说明理由.
如图,抛物线y=x2-4x+3与x轴交于A,B两点,且过点C(4,3),在对称轴右侧的抛物线上是否存在点P,使∠PAC>∠ACB,若存在,求出点P的横坐标xP的取值范围;若不存在,请说明理由.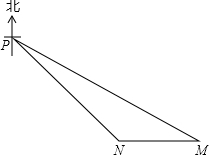 如图,某海岛上有一观测点P,一天上午9:00观测到一轮船在点M处,M在观测点P南偏东60°方向上,渔船由东向西匀速航行跟踪鱼群,当天上午9:30渔船行至点N处,N在观测点P的东南方向上,已知该渔船的速度为每小时40海里.
如图,某海岛上有一观测点P,一天上午9:00观测到一轮船在点M处,M在观测点P南偏东60°方向上,渔船由东向西匀速航行跟踪鱼群,当天上午9:30渔船行至点N处,N在观测点P的东南方向上,已知该渔船的速度为每小时40海里.