题目内容
16. 如图,
如图,(1)作△ABC的外接⊙O(用尺规作图,保留作图痕迹,不写作法);
(2)若AB=6cm,AC=BC=5cm,求⊙O的半径.
分析 (1)作线段AB于BC的垂直平分线相交于点O,则点O即为圆心,OA为半径,作△ABC的外接圆即可;
(2)先根据勾股定理求出CD的长,设OC=OA=r,则OD=CD-r,在Rt△AOD中,利用勾股定理求出r的值即可.
解答 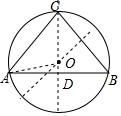 解:(1)如图,⊙O即为所求;
解:(1)如图,⊙O即为所求;
(2)∵AB=6cm,AC=BC=5cm,
∴AD=$\frac{1}{2}$AB=3cm,
∴CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4cm.
设OC=OA=r,则OD=4-r,
在Rt△AOD中,
∵AD2+OD2=OA2,即32+(4-r)2=r2,解得r=$\frac{25}{8}$.
点评 本题考查的是作图-复杂作图,熟知三角形外接圆的作法是解答此题的关键.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
1. 如图,正六边形ABCDEF内接于⊙O,过点O作OM⊥弦BC于点M,若⊙O的半径为4,则OM和$\widehat{BC}$的长分别为( )
如图,正六边形ABCDEF内接于⊙O,过点O作OM⊥弦BC于点M,若⊙O的半径为4,则OM和$\widehat{BC}$的长分别为( )
 如图,正六边形ABCDEF内接于⊙O,过点O作OM⊥弦BC于点M,若⊙O的半径为4,则OM和$\widehat{BC}$的长分别为( )
如图,正六边形ABCDEF内接于⊙O,过点O作OM⊥弦BC于点M,若⊙O的半径为4,则OM和$\widehat{BC}$的长分别为( )| A. | 2,$\frac{π}{3}$ | B. | 2$\sqrt{3}$,π | C. | $\sqrt{3}$,$\frac{2π}{3}$ | D. | 2$\sqrt{3}$,$\frac{4π}{3}$ |
5.已知第一个三角形的面积是1,它的三条中位线组成第1个三角形,第2个三角形的三条中位线又组成第3个三角形,以此类推…第2014个三角形的面积为( )
| A. | $\frac{1}{{2}^{4022}}$ | B. | $\frac{1}{{2}^{4024}}$ | C. | $\frac{1}{{2}^{4026}}$ | D. | $\frac{1}{{2}^{4028}}$ |
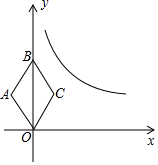 如图,在平面直角坐标系中,已知反比例函数y=$\frac{k}{x}$(x>0)的图象和菱形OABC,且OB=4,tan∠BOC=$\frac{1}{2}$.
如图,在平面直角坐标系中,已知反比例函数y=$\frac{k}{x}$(x>0)的图象和菱形OABC,且OB=4,tan∠BOC=$\frac{1}{2}$.
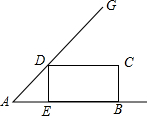 如图,∠A=45°,AB=30,点E在线段AB上运动,过点E作DE⊥AB,交AG于点D.以DE、EB为邻边作矩形BCDE.将△ADE沿直线DE翻折,使点A落在点F处.设矩形BCDE与△ADF重叠部分的面积为S,线段DE的长为x(0<x<30).
如图,∠A=45°,AB=30,点E在线段AB上运动,过点E作DE⊥AB,交AG于点D.以DE、EB为邻边作矩形BCDE.将△ADE沿直线DE翻折,使点A落在点F处.设矩形BCDE与△ADF重叠部分的面积为S,线段DE的长为x(0<x<30). 在平面直角坐标系中,点A和点B分别在x轴的正半轴和y轴的正半轴上,且OA=6,OB=8,点D是AB的中点.
在平面直角坐标系中,点A和点B分别在x轴的正半轴和y轴的正半轴上,且OA=6,OB=8,点D是AB的中点.