题目内容
17.已知x2-3x-1=0,求:(1)x2+$\frac{1}{{x}^{2}}$的值;
(2)(x-2)($\frac{1}{x}$+2)的值.
分析 根据x2-3x-1=0,两边同时除以x得到:x-3-$\frac{1}{x}$=0,从而得到x-$\frac{1}{x}$=3,然后变形求解即可.
解答 解:∵x2-3x-1=0,
∴两边同时除以x得到:x-3-$\frac{1}{x}$=0,
∴x-$\frac{1}{x}$=3,
(1)x2+$\frac{1}{{x}^{2}}$=(x-$\frac{1}{x}$)2+2=9+2=11;
(2)(x-2)($\frac{1}{x}$+2)=2(x-$\frac{1}{x}$)-3=2×3-3=3.
点评 本题考查了一元二次方程的解的知识及分式的混合运算,属于基础题,难度不大.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
5.已知第一个三角形的面积是1,它的三条中位线组成第1个三角形,第2个三角形的三条中位线又组成第3个三角形,以此类推…第2014个三角形的面积为( )
| A. | $\frac{1}{{2}^{4022}}$ | B. | $\frac{1}{{2}^{4024}}$ | C. | $\frac{1}{{2}^{4026}}$ | D. | $\frac{1}{{2}^{4028}}$ |
2.去年10月,国民体质监测中心等机构开展了青少年形体测评,专家组随机抽查了某市500名初中学生坐姿、站姿、走姿的好坏情况,数据如表:
我们要想知道每种形体占所抽查总人数的百分比,需对专家的测评数据作适当处理,画出适当的统计图,应选择什么统计图呢?
| 坐姿不良 | 站姿不良 | 走姿不良 | 三姿良好 |
| 100 | 155 | 185 | 60 |
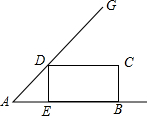 如图,∠A=45°,AB=30,点E在线段AB上运动,过点E作DE⊥AB,交AG于点D.以DE、EB为邻边作矩形BCDE.将△ADE沿直线DE翻折,使点A落在点F处.设矩形BCDE与△ADF重叠部分的面积为S,线段DE的长为x(0<x<30).
如图,∠A=45°,AB=30,点E在线段AB上运动,过点E作DE⊥AB,交AG于点D.以DE、EB为邻边作矩形BCDE.将△ADE沿直线DE翻折,使点A落在点F处.设矩形BCDE与△ADF重叠部分的面积为S,线段DE的长为x(0<x<30). 如图,在平面直角坐标系中,点A的坐标为(0,$\frac{29}{2}$),直线y=-$\frac{5}{12}$x-5与x轴、y轴分别交于B、C,点P是直线BC上的一个动点,则AP长的最小值为18.
如图,在平面直角坐标系中,点A的坐标为(0,$\frac{29}{2}$),直线y=-$\frac{5}{12}$x-5与x轴、y轴分别交于B、C,点P是直线BC上的一个动点,则AP长的最小值为18. 在平面直角坐标系中,点A和点B分别在x轴的正半轴和y轴的正半轴上,且OA=6,OB=8,点D是AB的中点.
在平面直角坐标系中,点A和点B分别在x轴的正半轴和y轴的正半轴上,且OA=6,OB=8,点D是AB的中点.