题目内容
6. 如图,已知AB∥CD,且$\frac{{S}_{△ABE}}{{S}_{△ADE}}$=$\frac{2}{3}$,求$\frac{{S}_{△ABE}}{{S}_{△DCE}}$的值.
如图,已知AB∥CD,且$\frac{{S}_{△ABE}}{{S}_{△ADE}}$=$\frac{2}{3}$,求$\frac{{S}_{△ABE}}{{S}_{△DCE}}$的值.
分析 由于△ABE和△ADE有共同的高,可得到$\frac{{S}_{△ABE}}{{S}_{△ADE}}$=$\frac{BE}{DE}$=$\frac{2}{3}$,由AB∥CD推出△ABE∽△DCE,根据相似三角形的性质即可证得结论.
解答 解:∵△ABE和△ADE有共同的高,
∴$\frac{{S}_{△ABE}}{{S}_{△ADE}}$=$\frac{BE}{DE}$=$\frac{2}{3}$,
∵AB∥CD,
∴△ABE∽△DCE,
∴$\frac{{S}_{△ABE}}{{S}_{△DCE}}$=$(\frac{BE}{DE})^{2}$=($\frac{2}{3}$)2=$\frac{4}{9}$.
点评 本题主要考查了相似三角形的判定和性质,三角形的面积公式,证得$\frac{BE}{DE}$=$\frac{2}{3}$是解题的关键.

练习册系列答案
相关题目
16. 如图,在△ABO中,两个顶点A、B的坐标分别为A(6,6),B(8,2),线段CD是以O为位似中心,在第一象限内将线段AB缩小为原来的一半后得到线段,则端点D的坐标为( )
如图,在△ABO中,两个顶点A、B的坐标分别为A(6,6),B(8,2),线段CD是以O为位似中心,在第一象限内将线段AB缩小为原来的一半后得到线段,则端点D的坐标为( )
 如图,在△ABO中,两个顶点A、B的坐标分别为A(6,6),B(8,2),线段CD是以O为位似中心,在第一象限内将线段AB缩小为原来的一半后得到线段,则端点D的坐标为( )
如图,在△ABO中,两个顶点A、B的坐标分别为A(6,6),B(8,2),线段CD是以O为位似中心,在第一象限内将线段AB缩小为原来的一半后得到线段,则端点D的坐标为( )| A. | (3,3) | B. | (4,3) | C. | (3,1) | D. | (4,1) |
17.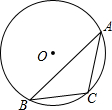 如图,△ABC内接于⊙O,BC=8,⊙O半径为5,则sinA的值为( )
如图,△ABC内接于⊙O,BC=8,⊙O半径为5,则sinA的值为( )
 如图,△ABC内接于⊙O,BC=8,⊙O半径为5,则sinA的值为( )
如图,△ABC内接于⊙O,BC=8,⊙O半径为5,则sinA的值为( )| A. | $\frac{3}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
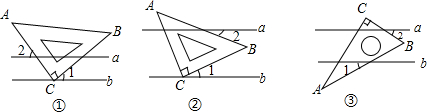
15.顺次连接四边形ABCD四条边的中点所得的四边形是菱形,则四边形ABCD一定是( )
| A. | 平行四边形 | B. | 矩形 | ||
| C. | 对角线相互垂直的四边形 | D. | 对角线相等的四边形 |
 在一次暖气管道的铺设工程中,由点A出发沿正西方向进行,在点A的南偏西55°的方向上有一个敬老院B,占地是以B为中心方圆100m的圆,当工程进行了200m后到达C处,此时B在C南偏西25°的方向上.请你根据题中所提供的信息计算并分析一下,工程继续进行下去,是否会穿越敬老院.
在一次暖气管道的铺设工程中,由点A出发沿正西方向进行,在点A的南偏西55°的方向上有一个敬老院B,占地是以B为中心方圆100m的圆,当工程进行了200m后到达C处,此时B在C南偏西25°的方向上.请你根据题中所提供的信息计算并分析一下,工程继续进行下去,是否会穿越敬老院.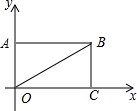 如图,矩形ABCO,∠BOC=30°,OB=4,则点A的坐标为(0,2),点B的坐标为(2$\sqrt{3}$,2).
如图,矩形ABCO,∠BOC=30°,OB=4,则点A的坐标为(0,2),点B的坐标为(2$\sqrt{3}$,2).