题目内容
解方程:
(1)(x-3)2-9=0;
(2)x2-2x=2x+1;
(3)(x+1)(x-1)+2(x+3)=8.
(1)(x-3)2-9=0;
(2)x2-2x=2x+1;
(3)(x+1)(x-1)+2(x+3)=8.
考点:解一元二次方程-配方法,解一元二次方程-直接开平方法
专题:
分析:(1)根据开平方的方法,可得方程的解;
(2)根据公式法,可得方程的解;
(3)根据因式分解,可得方程解.
(2)根据公式法,可得方程的解;
(3)根据因式分解,可得方程解.
解答:解:(1)移项,得(x-3)2=9,
开方,得x-3=±3,
x1=0,x2=6
(2)化成一般形式x2-4x-1=0,
a=1,b=-4,c=-1,
△=b2-4ac=(-4)2-4×1×(-1)=20,
x=
=2±
,
x1=2+
,x2=2-
;
(3)化成一般形式x2+2x-3=0,
因式分解,得(x-1)(x+3)=0.
解得x1=1,x2=-3
开方,得x-3=±3,
x1=0,x2=6
(2)化成一般形式x2-4x-1=0,
a=1,b=-4,c=-1,
△=b2-4ac=(-4)2-4×1×(-1)=20,
x=
-b±
| ||
| 2a |
| 5 |
x1=2+
| 5 |
| 5 |
(3)化成一般形式x2+2x-3=0,
因式分解,得(x-1)(x+3)=0.
解得x1=1,x2=-3
点评:本题考查了解一元二次方程,(1)用直接开方法求一元二次方程的解的类型有:x2=a(a≥0);ax2=b(a,b同号且a≠0);(x+a)2=b(b≥0);a(x+b)2=c(a,c同号且a≠0).法则:要把方程化为“左平方,右常数,先把系数化为1,再开平方取正负,分开求得方程解”.
(2)运用整体思想,会把被开方数看成整体.
(3)用直接开方法求一元二次方程的解,要仔细观察方程的特点.
(2)运用整体思想,会把被开方数看成整体.
(3)用直接开方法求一元二次方程的解,要仔细观察方程的特点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
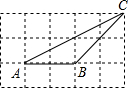 如图,在5×3的网格中,每格小正方形的边长都是1,若△ABC的三个顶点都在相应格点上,则sin∠CAB的值为( )
如图,在5×3的网格中,每格小正方形的边长都是1,若△ABC的三个顶点都在相应格点上,则sin∠CAB的值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,在△ABC中,AC=BC,CD为AB边上的中线,DE⊥CB于E,∠B=55°,求∠CDE的度数.
如图,在△ABC中,AC=BC,CD为AB边上的中线,DE⊥CB于E,∠B=55°,求∠CDE的度数. (2)如图,已知∠ABC=90°,AB=πr,BC=
(2)如图,已知∠ABC=90°,AB=πr,BC=