题目内容
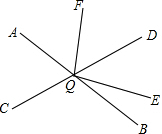 如图,直线AB,CD相交于点O,∠DOE:∠BOE=4:1,OF平分∠AOD,∠AOC=∠AOF-15°,求∠EOF的度数.
如图,直线AB,CD相交于点O,∠DOE:∠BOE=4:1,OF平分∠AOD,∠AOC=∠AOF-15°,求∠EOF的度数.考点:对顶角、邻补角
专题:
分析:首先根据角平分线的性质可得∠AOF=∠FOD=
∠AOD,再根据邻补角互补可得∠AOF-15°+2∠AOF=180°,计算出∠AOF的度数,进而可得∠AOC的度数,再根据∠DOE:∠BOE=4:1可得∠DOE的度数,进而可得答案.
| 1 |
| 2 |
解答: 解:∵OF平分∠AOD,
解:∵OF平分∠AOD,
∴∠AOF=∠FOD=
∠AOD,
∵∠AOC=∠AOF-15°,∠AOC+∠AOD=180°,
∴∠AOF-15°+2∠AOF=180°,
解得:∠AOF=65°,
∴∠A0C=65°-15°=50°,
∠BOD=50°,
∵∠DOE:∠BOE=4:1,
∴∠DOE=40°,
∴∠EOF=40°+65°=105°.
 解:∵OF平分∠AOD,
解:∵OF平分∠AOD,∴∠AOF=∠FOD=
| 1 |
| 2 |
∵∠AOC=∠AOF-15°,∠AOC+∠AOD=180°,
∴∠AOF-15°+2∠AOF=180°,
解得:∠AOF=65°,
∴∠A0C=65°-15°=50°,
∠BOD=50°,
∵∠DOE:∠BOE=4:1,
∴∠DOE=40°,
∴∠EOF=40°+65°=105°.
点评:此题主要考查了邻补角和对顶角,关键是掌握邻补角互补,对顶角相等.

练习册系列答案
 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 下图描述了小丽散步过程中离家的距离s(米)与散步所用时间t(分)之间的函数关系.依据图象,下面描述符合小红散步情景的是( )
下图描述了小丽散步过程中离家的距离s(米)与散步所用时间t(分)之间的函数关系.依据图象,下面描述符合小红散步情景的是( )| A、从家出发,到了一个公共阅报栏,看了一会儿报,就回家了 |
| B、从家出发,到了一个公共阅报栏,看了一会儿报后,继续向前走了一段,然后回家了 |
| C、从家出发,一直散步(没有停留),然后回家了 |
| D、从家出发,散了一会儿步,就找同学去了,18分钟后才开始返回 |
下列函数中,y随x的增大而增大的是( )
| A、y=-2x+3 | ||
B、y=-
| ||
C、y=
| ||
| D、y=-2x2(x>0) |
(
)-1的计算结果为( )
| 1 |
| 2 |
A、
| ||
| B、-2 | ||
| C、2 | ||
D、-
|
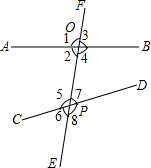 如图,直线AB,CD与直线EF分别交于点O,P.
如图,直线AB,CD与直线EF分别交于点O,P. 函数y=ax2与直线y=-2x-4交于点(2,b).
函数y=ax2与直线y=-2x-4交于点(2,b). 某几何体的三视图如图所示,其中主视图中半圆的半径为1.
某几何体的三视图如图所示,其中主视图中半圆的半径为1.