题目内容
20. 如图,已知四边形ABCD是长方形,△DCE是等边三角形,A(0,0),B(4,0),D(0,2),求E点的坐标.
如图,已知四边形ABCD是长方形,△DCE是等边三角形,A(0,0),B(4,0),D(0,2),求E点的坐标.
分析 得出两种情况,当E在DC的上方时,当E在CD的下方时,过E作EF⊥DC于F,求出DF和EF,即可得出E的坐标.
解答 解:分为两种情况:如图,当E在DC的上方时,
过E作EF⊥DC于F,
∵A(0,0),B(4,0),D(0,2),四边形ABCD是矩形,
∴DC=AB=4,AD=BC=2,
∵△DCE是等边三角形,
∴DE=DC=EC=4,DF=FC=2,
在Rt△DFE中,由勾股定理得:EF=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
即E的坐标为(2,2+2$\sqrt{2}$),
当E在CD的下方时,E的坐标为(2,2$\sqrt{3}$-2).
点评 本题考查了矩形的性质,等边三角形的性质,点的坐标等知识点,能求出符合的所有情况是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
8.我国属于水资源缺乏的国家之一,节约用水,人人有责.某市为了强化公民的节水意思,合理利用水资源,采用价格调控手段达到节水的目的,该市自来水价格表如下:
注:水费按月结算
(1)若某户居民3月份用水4m3,则应缴水费12元;
(2)若某户居民4月份用水8m3,求应缴水费多少元?
(3)若某户居民8月份用水xm3(其中x大于5),求应缴水费多少元?(用含x的式子表示)
(4)若某户居民9月份用水18m3,则应缴水费多少元?
| 每月用水量 | 单价 |
| 不超过5m3 | 3元/m3 |
| 超过5m3不超过10m3的部分 | 5元/m3 |
| 超过10m3的部分 | 8元/m3 |
(1)若某户居民3月份用水4m3,则应缴水费12元;
(2)若某户居民4月份用水8m3,求应缴水费多少元?
(3)若某户居民8月份用水xm3(其中x大于5),求应缴水费多少元?(用含x的式子表示)
(4)若某户居民9月份用水18m3,则应缴水费多少元?
15.一直角三角形的两直角边长为3和4,则第三边长为( )
| A. | $\sqrt{7}$ | B. | 5 | C. | $\sqrt{7}$或5 | D. | 7 |
5. 如图所示的图形是正方体的一种平面展开图,它各面上部标有数字,则数字-2的面与它对面数字之积是( )
如图所示的图形是正方体的一种平面展开图,它各面上部标有数字,则数字-2的面与它对面数字之积是( )
 如图所示的图形是正方体的一种平面展开图,它各面上部标有数字,则数字-2的面与它对面数字之积是( )
如图所示的图形是正方体的一种平面展开图,它各面上部标有数字,则数字-2的面与它对面数字之积是( )| A. | -10 | B. | 10 | C. | -8 | D. | 8 |
9.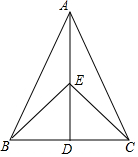 如图,在△ABC中,AB=AC,EB=EC,下列判定不正确的是( )
如图,在△ABC中,AB=AC,EB=EC,下列判定不正确的是( )
 如图,在△ABC中,AB=AC,EB=EC,下列判定不正确的是( )
如图,在△ABC中,AB=AC,EB=EC,下列判定不正确的是( )| A. | △ABD≌△ACE | B. | △ABE≌△ACE | C. | △BDE≌△CDE | D. | △ABD≌△ACD |
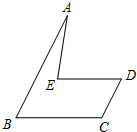 如图,已知AB∥CD,BC∥DE,若∠A=20°,∠C=120°,求∠AED的度数.
如图,已知AB∥CD,BC∥DE,若∠A=20°,∠C=120°,求∠AED的度数.
 如图,已知二次函数y=-x2+2x+m图象过点A(3,0),与y轴交于点B
如图,已知二次函数y=-x2+2x+m图象过点A(3,0),与y轴交于点B