题目内容
6．
如图，直线a∥b，AB⊥BC，∠1=40°，则∠2的度数为（ ）| A． | 30° | B． | 40° | C． | 50° | D． | 60° |
分析 先根据平行线的性质求出∠ACB的度数，再由垂直的定义得出∠ABC的度数，根据三角形内角和定理即可得出结论．
解答 解：∵直线a∥b，∠1=40°，
∴∠ACB=∠1=40°．
∵AB⊥BC，
∴∠ABC=90°，
∴∠2=90°-∠ACB=90°-40°=50°．
故选C．
点评 本题考查的是平行线的性质，用到的知识点为：两直线平行，同位角相等．
练习册系列答案
口算心算速算应用题系列答案
同步拓展阅读系列答案
相关题目
如图，在等边△ABC的BC边为直径画半圆，分别交AB、AC于点E、D，等边三角形的边长是8．在边AB上取一点F，使AF=2，连接FD．求证：
的根是（ ）
B. 
C. 
D. 
14．
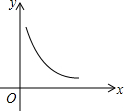如图中的曲线是反比例函数y=$\frac{m+5}{x}$图象的一支，则m的取值范围是（ ）
如图中的曲线是反比例函数y=$\frac{m+5}{x}$图象的一支，则m的取值范围是（ ）| A． | m＞-5 | B． | 0＜m＜5 | C． | -5＜m＜0 | D． | m＜-5 |
1．甲、乙两商场同时开业，为了吸引顾客，都举办有奖酬宾活动，凡购物满100元，均可得到一次摸奖的机会．在一个纸盒里装有2个红球和2个白球，除颜色外，其他全部相同，摸奖者一次从中摸出两个球，根据球的颜色决定送礼金券的多少（如下表）．
甲商场：
乙商场：
（1）请你用列表法（或画树状图）求出摸到一红一白的概率；
（2）如果只考虑中奖因素，你将会选择去哪个商场购物？请说明理由．
甲商场：
| 球 | 两红 | 一红一白 | 两白 |
| 礼金券（元） | 5 | 10 | 5 |
| 球 | 两红 | 一红一白 | 两白 |
| 礼金券（元） | 10 | 5 | 10 |
（2）如果只考虑中奖因素，你将会选择去哪个商场购物？请说明理由．
11．
如图，AB为⊙O的直径，C为⊙O外一点，过点C作⊙O的切线，切点为B，连接AC交⊙O于点D，∠C=40°，点E在AB左侧的半圆上运动（不与A、B重合），则∠AED的大小是（ ）
如图，AB为⊙O的直径，C为⊙O外一点，过点C作⊙O的切线，切点为B，连接AC交⊙O于点D，∠C=40°，点E在AB左侧的半圆上运动（不与A、B重合），则∠AED的大小是（ ）| A． | 20° | B． | 40° | C． | 50° | D． | 80° |
16．
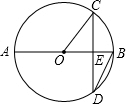如图，AB是⊙O的直径，⊙O的半径$\sqrt{3}$cm，弦CD⊥AB于E，∠CDB=30°，则弦CD的长为（ ）
如图，AB是⊙O的直径，⊙O的半径$\sqrt{3}$cm，弦CD⊥AB于E，∠CDB=30°，则弦CD的长为（ ）| A． | $\frac{3}{2}$cm | B． | 3cm | C． | 2$\sqrt{3}$cm | D． | 9cm |