题目内容
5.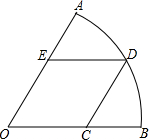 如图,扇形AOB的圆心角为60°,边长为$\sqrt{3}$的菱形OCDE的顶点C,E,D分别在OB,OA,弧AB上,则扇形AOB的面积为$\frac{3}{2}$π.(结果保留π)
如图,扇形AOB的圆心角为60°,边长为$\sqrt{3}$的菱形OCDE的顶点C,E,D分别在OB,OA,弧AB上,则扇形AOB的面积为$\frac{3}{2}$π.(结果保留π)
分析 根据菱形的性质结合锐角三角函数关系得出DF,DO的长,再利用扇形面积公式求出即可.
解答 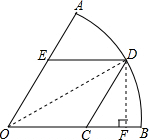 解:连接DO,过点D作DF⊥OB于点F,
解:连接DO,过点D作DF⊥OB于点F,
∵扇形AOB的圆心角为60°,边长为$\sqrt{3}$的菱形OCDE,
∴CO=CD=$\sqrt{3}$,∠DOB=30°,∠DCF=60°,
故sin60°=$\frac{DF}{DC}$=$\frac{DF}{\sqrt{3}}$,
则DF=$\frac{3}{2}$,
∴DO=3,
∴扇形AOB的面积为:$\frac{60π×{3}^{2}}{360}$=$\frac{3}{2}$π.
故答案为:$\frac{3}{2}$π.
点评 此题主要考查了菱形的性质以及锐角三角函数关系以及扇形面积公式,得出DO的长是解题关键.

练习册系列答案
 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案
相关题目
16.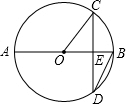 如图,AB是⊙O的直径,⊙O的半径$\sqrt{3}$cm,弦CD⊥AB于E,∠CDB=30°,则弦CD的长为( )
如图,AB是⊙O的直径,⊙O的半径$\sqrt{3}$cm,弦CD⊥AB于E,∠CDB=30°,则弦CD的长为( )
 如图,AB是⊙O的直径,⊙O的半径$\sqrt{3}$cm,弦CD⊥AB于E,∠CDB=30°,则弦CD的长为( )
如图,AB是⊙O的直径,⊙O的半径$\sqrt{3}$cm,弦CD⊥AB于E,∠CDB=30°,则弦CD的长为( )| A. | $\frac{3}{2}$cm | B. | 3cm | C. | 2$\sqrt{3}$cm | D. | 9cm |
20.如图1,在等边△ABC中,点E、D分别是AC,BC边的中点,点P为AB边上的一个动点,连接PE,PD,PC,DE.设AP=x,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )
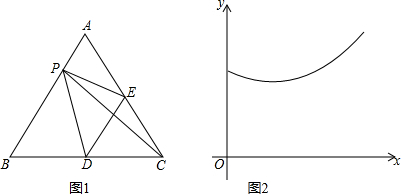

| A. | 线段PD | B. | 线段PC | C. | 线段PE | D. | 线段DE |
10.2015年1月24日,“贵广大庙会”在贵阳观山湖区正式面向市民开发,第一次就有近5.6×104人到场购置年货,5.6×104可以表示为( )
| A. | 56 | B. | 560 | C. | 5600 | D. | 56000 |
15.下列运算正确的是( )
| A. | (a3-a)÷a=a2 | B. | (a3)2=a5 | C. | a3+a2=a5 | D. | a3÷a3=1 |
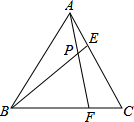 如图,等边三角形ABC的边长为6,点E、点F分别是AC、BC边上的点,连接AF,BE交于点P.给出以下判断:
如图,等边三角形ABC的边长为6,点E、点F分别是AC、BC边上的点,连接AF,BE交于点P.给出以下判断: