Question

13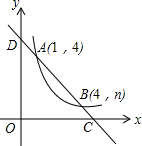．如图，直线y=ax+b与反比例函数y=$\frac{m}{x}$（x＞0）的图象交于A（1，4），B（4，n）两点，与x轴、y轴分别交于C、D两点．
（1）m=4，n=1；若M（x₁，y₁），N（x₂，y₂）是反比例函数图象上两点，且0＜x₁＜x₂，则y₁＞y₂（填“＜”或“=”或“＞”）；
（2）若线段CD上的点P到x轴、y轴的距离相等，求点P的坐标．

Answer 1

分析 （1）由点A的坐标利用反比例函数图象上点的坐标特征即可得出m的值，再由点B也在反比例函数图象上即可得出n的值，由反比例函数系数m的值结合反比例函数的性质即可得出反比例函数的增减性，由此即可得出结论；
（2）设过C、D点的直线解析式为y=kx+b，由点A、B的坐标利用待定系数法即可求出直线CD的解析式，设出点P的坐标为（t，-t+5），由点P到x轴、y轴的距离相等即可得出关于t的含绝对值符号的一元一次方程，解方程即可得出t的值，从而得出点P的坐标．

解答 解：（1）∵反比例函数y=$\frac{m}{x}$（x＞0）的图象过点A（1，4），
∴m=1×4=4．
∵点B（4，n）在反比例函数y=$\frac{4}{x}$的图象上，
∴m=4n=4，解得：n=1．
∵在反比例函数y=$\frac{4}{x}$（x＞0）中，m=4＞0，
∴反比例函数y=$\frac{4}{x}$的图象单调递减，
∵0＜x₁＜x₂，
∴y₁＞y₂．
故答案为：4；1；＞．
（2）设过C、D点的直线解析式为y=kx+b，
∵直线CD过点A（1，4）、B（4，1）两点，
∴$\left\{\begin{array}{l}{4=k+b}\\{1=4k+b}\end{array}\right.$，解得：$\left\{\begin{array}{l}{k=-1}\\{b=5}\end{array}\right.$，
∴直线CD的解析式为y=-x+5．
设点P的坐标为（t，-t+5），
∴|t|=|-t+5|，
解得：t=$\frac{5}{2}$．
∴点P的坐标为（$\frac{5}{2}$，$\frac{5}{2}$）．

点评 本题考查了反比例函数图象上点的坐标特征、反比例函数与一次函数的交点问题、反比例函数的性质以及解含绝对值符号的一元一次方程，解题的关键是：（1）求出m的值；（2）找出关于t的含绝对值符号的一元一次方程．本题属于基础题，难度不大，解决该题型题目时，结合点的坐标利用待定系数法求出函数的解析式是关键．