题目内容
3.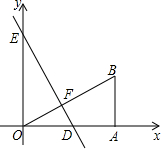 如图,Rt△AOB的顶点O与原点重合,直角顶点A在x轴上,顶点B的坐标为(4,3),直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点D、E,交OB于点F.
如图,Rt△AOB的顶点O与原点重合,直角顶点A在x轴上,顶点B的坐标为(4,3),直线y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点D、E,交OB于点F.(1)写出图中的全等三角形及理由;
(2)求OF的长.
分析 (1)先求出D、E两点的坐标,进而可得出OD、OE的长,再由B点坐标可得出OA,AB的长,由此可得出结论;
(2)先根据全等三角形的性质得出∠AOB=∠OED,再由余角的定义得出OF⊥ED,由勾股定理得出ED的长,再由三角形的面积公式即可得出结论.
解答 解:(1)△AOB≌△OED.
理由:∵y=-$\frac{4}{3}$x+4与x轴、y轴分别交于点D、E,
∴D(3,0),E(0,4),
∴OD=3,OE=4.
∵B(4,3),
∴OA=4,AB=3.
在△AOB与△OED中,
∵$\left\{\begin{array}{l}{AB=OD}\\{∠OAB=∠DOE=90°}\\{OA=OE}\end{array}\right.$,
∴△AOB≌△OED(SAS);
(2)∵△AOB≌△OED,
∴∠AOB=∠OED.
∵∠AOB+∠EOF=90°,
∴∠OED+∠EOF=90°,
∴∠OFE=90°,
∴OF⊥ED.
在Rt△ODE中,ED=$\sqrt{O{E}^{2}+O{D}^{2}}$=$\sqrt{{4}^{2}+{3}^{2}}$=5,
∵S△ODE=$\frac{1}{2}$OD•OE=$\frac{1}{2}$DE•OF=6,
∴OF=$\frac{12}{5}$.
点评 本题考查的是一次函数图象上点的坐标特点,熟知一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,点C在线段AB上,AC=6cm,MB=10cm,点M,N分别为AC,BC的中点.
如图,点C在线段AB上,AC=6cm,MB=10cm,点M,N分别为AC,BC的中点.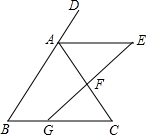 如图,在△ABC中,已知点D在线段AB的反向延长线上,过AC的中点F作线段GE交∠DAC的平分线于E,交BC于G,且AE∥BC.
如图,在△ABC中,已知点D在线段AB的反向延长线上,过AC的中点F作线段GE交∠DAC的平分线于E,交BC于G,且AE∥BC.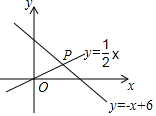 (1)计算(2$\sqrt{3}$-1)2
(1)计算(2$\sqrt{3}$-1)2 已知某四棱柱的俯视图如图所示,画出它的主视图和左视图.
已知某四棱柱的俯视图如图所示,画出它的主视图和左视图.