题目内容
 如图,在水上治安指挥塔A西侧两条航线l1、l2上有两艘巡逻艇B与C(C所在航线靠近A),直线l1、l2间的距离CD=
如图,在水上治安指挥塔A西侧两条航线l1、l2上有两艘巡逻艇B与C(C所在航线靠近A),直线l1、l2间的距离CD=| 3 |
(1)巡逻艇C与塔A之间的距离AC.(结果保留根号)
(2)已知巡逻艇C的速度每小时比巡逻艇B快5km,当两艘巡逻艇同时到达指挥塔A的正南方向时,求巡逻艇B的速度.
考点:解直角三角形的应用-方向角问题
专题:
分析:(1)可先由AB及方向角南偏西30°得出AF的长,再减去CD的长得AE的长,又A在C的北偏东60°方向上,得出AC的长;
(2)设巡逻艇B的速度为xkm/小时,则巡逻艇C的速度为(x+5)km/小时,根据两艘巡逻艇同时到达指挥塔A的正南方向可列方程求解即可.
(2)设巡逻艇B的速度为xkm/小时,则巡逻艇C的速度为(x+5)km/小时,根据两艘巡逻艇同时到达指挥塔A的正南方向可列方程求解即可.
解答:解:由题意可得:四边形CDFE是矩形,故EF=CD=
km,
在Rt△ABF中,cos30°=
,
∴AF=ABcos30°=6×
=3
,
∴AE=AF-EF=3
-
=2
,
在Rt△AEC中,∠ACE=30°,
∴sin30°=
,即AC=
=4
.
答:巡逻艇C与塔A之间的距离AC为4
km;
(2)在Rt△AEC中,∠ACE=30°,AC=4
.
∴CE=6km,
在Rt△ABF中,∠BAF=30°,AB=6km,
∴BF=3km,
设巡逻艇B的速度为xkm/小时,则巡逻艇C的速度为(x+5)km/小时,依题意有
=
,
解得x=5,
经检验可知x=5是原方程的解.
故巡逻艇B的速度是5km/小时.
| 3 |
在Rt△ABF中,cos30°=
| AF |
| AB |
∴AF=ABcos30°=6×
| ||
| 2 |
| 3 |
∴AE=AF-EF=3
| 3 |
| 3 |
| 3 |
在Rt△AEC中,∠ACE=30°,
∴sin30°=
| AE |
| AC |
| AE |
| sin30° |
| 3 |
答:巡逻艇C与塔A之间的距离AC为4
| 3 |
(2)在Rt△AEC中,∠ACE=30°,AC=4
| 3 |
∴CE=6km,
在Rt△ABF中,∠BAF=30°,AB=6km,
∴BF=3km,
设巡逻艇B的速度为xkm/小时,则巡逻艇C的速度为(x+5)km/小时,依题意有
| 6 |
| x+5 |
| 3 |
| x |
解得x=5,
经检验可知x=5是原方程的解.
故巡逻艇B的速度是5km/小时.
点评:本题主要考查了方向角的含义,正确记忆三角函数的定义是解决本题的关键.同时考查了分式方程,分式方程注意要验根.

练习册系列答案
相关题目
若正方形的对角线长为
,则它的面积为( )
| 2 |
| A、1 | ||
B、
| ||
| C、2 | ||
D、2
|
若方程x2+px-q=0的二根为x1,x2且x1>1,p+q+3>0,则x2( )
| A、小于1 | B、等于1 |
| C、大于1 | D、不能确定 |
 如图,AE平分∠BAC,△AEC沿EC折叠,A恰好落在BC边上,且BD=DE.若∠C=60°,则∠B的度数为( )
如图,AE平分∠BAC,△AEC沿EC折叠,A恰好落在BC边上,且BD=DE.若∠C=60°,则∠B的度数为( )| A、30° | B、40° |
| C、45° | D、60° |
已知2x=8,2y=4,则2y-x=( )
| A、-2 | ||
B、-
| ||
| C、2 | ||
D、
|
下列各选项中,是无理数的是( )
| A、-3 | ||
| B、0 | ||
C、
| ||
D、
|
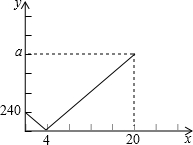 A、B与C三地依次在一条直线上.甲,乙两人同时分别从A,B两地沿直线匀速步行到C地,甲到达C地花了20分钟.设两人出发x(分钟)时,甲离B地的距离为y(米),y与x的函数图象如图所示.
A、B与C三地依次在一条直线上.甲,乙两人同时分别从A,B两地沿直线匀速步行到C地,甲到达C地花了20分钟.设两人出发x(分钟)时,甲离B地的距离为y(米),y与x的函数图象如图所示.