题目内容
 如图,AE平分∠BAC,△AEC沿EC折叠,A恰好落在BC边上,且BD=DE.若∠C=60°,则∠B的度数为( )
如图,AE平分∠BAC,△AEC沿EC折叠,A恰好落在BC边上,且BD=DE.若∠C=60°,则∠B的度数为( )| A、30° | B、40° |
| C、45° | D、60° |
考点:翻折变换(折叠问题)
专题:
分析:连接BE.根据折叠的性质和已知条件“AE平分∠BAC”知点E是△ABC的内角平分线的交点.设∠5=∠6=x°由等腰△BDE、△BDE的外角定理求得∠EDC=∠5+∠7=2x°
然后根据△ABC的内角和定理列出关于x的方程,通过方程来解答.
然后根据△ABC的内角和定理列出关于x的方程,通过方程来解答.
解答: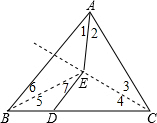 解:由折叠的性质知,∠3=∠4,即CE是∠ACB的平分线.
解:由折叠的性质知,∠3=∠4,即CE是∠ACB的平分线.
又∵AE平分∠BAC,根据三角形三条角平分线交于一点,
∴连结BE,则BE平分∠ABC.
设∠5=∠6=x°,
∴∠ABC=2x°.
∵BD=DE
∴∠5=∠7=x°
由三角形外角性质可知
∠EDC=∠5+∠7=2x°
∴∠2=∠EDC=2x°∴∠BAC=4x°
由三角形内角和定理知:
∠ABC+∠BAC+∠ACB=180°
∴2x°+4x°+60°=180°
解得 x=20°
∴∠B=2x=40°
故选B.
 解:由折叠的性质知,∠3=∠4,即CE是∠ACB的平分线.
解:由折叠的性质知,∠3=∠4,即CE是∠ACB的平分线.又∵AE平分∠BAC,根据三角形三条角平分线交于一点,
∴连结BE,则BE平分∠ABC.
设∠5=∠6=x°,
∴∠ABC=2x°.
∵BD=DE
∴∠5=∠7=x°
由三角形外角性质可知
∠EDC=∠5+∠7=2x°
∴∠2=∠EDC=2x°∴∠BAC=4x°
由三角形内角和定理知:
∠ABC+∠BAC+∠ACB=180°
∴2x°+4x°+60°=180°
解得 x=20°
∴∠B=2x=40°
故选B.
点评:本题考查了折叠的性质.折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
x,y都是质数,则方程x+y=1999共有( )
| A、1组解 | B、2组解 |
| C、3组解 | D、4组解 |
下列命题中,真命题是( )
| A、矩形的对角线相互垂直 |
| B、顺次连接平行四边形各边中点所得到的四边形是矩形 |
| C、等腰梯形的对角线互相垂直且相等 |
| D、对角线互相垂直平分的四边形是菱形 |
在某次国际乒乓球单打比赛中,甲、乙两名中国选手进入最后决赛,那么在这次比赛中,事件“冠军属于中国选手”为( )
| A、必然事件 | B、不可能事件 |
| C、随机事件 | D、可能事件 |
已知⊙O的直径是10,圆心O到直线l的距离是5,则直线l和⊙O的位置关系是( )
| A、相离 | B、相交 | C、相切 | D、外切 |
 如图,在水上治安指挥塔A西侧两条航线l1、l2上有两艘巡逻艇B与C(C所在航线靠近A),直线l1、l2间的距离CD=
如图,在水上治安指挥塔A西侧两条航线l1、l2上有两艘巡逻艇B与C(C所在航线靠近A),直线l1、l2间的距离CD= 如图,AB为⊙O的直径,AC为⊙O的弦,∠BAC的平分线交⊙O于点D,DE⊥AC于点E.
如图,AB为⊙O的直径,AC为⊙O的弦,∠BAC的平分线交⊙O于点D,DE⊥AC于点E. 小明参加数学组的活动,想测量一座山的高度,于是他们在山前D处测得山顶C的仰角为30°,向前走200米来到山脚A处,测得山坡AC的坡度为i=1:0.5.若忽略测角仪的高度,请问他们通过这些数据可以计算出山的高度吗?若能,请你帮忙算一算,结果保留整数.(参考数据:
小明参加数学组的活动,想测量一座山的高度,于是他们在山前D处测得山顶C的仰角为30°,向前走200米来到山脚A处,测得山坡AC的坡度为i=1:0.5.若忽略测角仪的高度,请问他们通过这些数据可以计算出山的高度吗?若能,请你帮忙算一算,结果保留整数.(参考数据: