题目内容
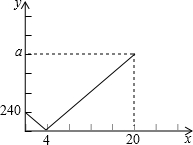 A、B与C三地依次在一条直线上.甲,乙两人同时分别从A,B两地沿直线匀速步行到C地,甲到达C地花了20分钟.设两人出发x(分钟)时,甲离B地的距离为y(米),y与x的函数图象如图所示.
A、B与C三地依次在一条直线上.甲,乙两人同时分别从A,B两地沿直线匀速步行到C地,甲到达C地花了20分钟.设两人出发x(分钟)时,甲离B地的距离为y(米),y与x的函数图象如图所示.(1)甲的速度为
(2)已知乙的步行速度是40米/分钟,设乙步行时与B地的距离为y1(米),直接写出y1与x的函数关系式,并在图中画出y1(米)与x(分钟)的大致函数图象(友情提醒:标出线段的端点坐标);
(3)乙出发几分钟后两人在途中相遇?
考点:一次函数的应用
专题:
分析:(1)根据图象速度=路程÷时间就可以求出甲的速度,根据路程=速度×时间久可以求出a的值,从而可以求出AC之间的距离;
(2)先用(1)的结论求出乙走到C地的时间,用待定系数法就可以求出y1的解析式,从而可以画出大致图形;
(3)如图1,求出BC的解析式,再与y1构成方程组求出其解就可以得出结论.
(2)先用(1)的结论求出乙走到C地的时间,用待定系数法就可以求出y1的解析式,从而可以画出大致图形;
(3)如图1,求出BC的解析式,再与y1构成方程组求出其解就可以得出结论.
解答:解:(1)由图象得:
甲的速度为:240÷4=60米/分,
a=(20-4)×60=960米,
∴AC的距离为:240+960=1200米;
(2)由题意,得
960÷40=24,
∴y1经过(24,960)这点,设y1的解析式为y1=kx,
960=24k,
k=40,
∴y1的解析式为y1=40x.
画出大致图象为:
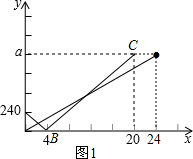
(3)由图1得线段BC经过(4,0),(20,960)这两点,设BC的解析式为y=kx+b,由图象得
,
解得:
,
∴y=60x-240,
∴
,
解得:x=12.
答:乙出发12分钟后两人相遇.
故答案为:60,960米,1200.
甲的速度为:240÷4=60米/分,
a=(20-4)×60=960米,
∴AC的距离为:240+960=1200米;
(2)由题意,得
960÷40=24,
∴y1经过(24,960)这点,设y1的解析式为y1=kx,
960=24k,
k=40,
∴y1的解析式为y1=40x.
画出大致图象为:

(3)由图1得线段BC经过(4,0),(20,960)这两点,设BC的解析式为y=kx+b,由图象得
|
解得:
|
∴y=60x-240,
∴
|
解得:x=12.
答:乙出发12分钟后两人相遇.
故答案为:60,960米,1200.
点评:本题考查了路程=速度×时间的运用,待定系数法求函数的解析式的运用,由函数的解析式画函数图象的运用,一次函数与二元一次方程组的运用.解答时求出一次函数的解析式是关键.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
已知函数y=
的图象经过点(2,3),那么图象应在( )
| k |
| x |
| A、第一、三象限 |
| B、第一、二象限 |
| C、第二、四象限 |
| D、第三、四象限 |
 某大公司“五一”节慰问公司全体职工,决定到一果园一次性采购一种水果,其采购价y(元/吨)与采购量x(吨)之间的关系图象如图中折线ABC(不包括端点A、但包括端点C).
某大公司“五一”节慰问公司全体职工,决定到一果园一次性采购一种水果,其采购价y(元/吨)与采购量x(吨)之间的关系图象如图中折线ABC(不包括端点A、但包括端点C). 如图,在水上治安指挥塔A西侧两条航线l1、l2上有两艘巡逻艇B与C(C所在航线靠近A),直线l1、l2间的距离CD=
如图,在水上治安指挥塔A西侧两条航线l1、l2上有两艘巡逻艇B与C(C所在航线靠近A),直线l1、l2间的距离CD=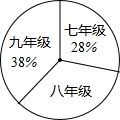 “读书好,读好书,好读书.”阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.为了培养学生的读书习惯,某校组织学生开展“绿色大阅读”活动.右图是在活动之初某校对三个年级学生信息做的一个调查.图1是人数分布扇形统计图,其中八年级人数为408人,表2是该校学生阅读课外书籍情况统计表.请你根据图表中的信息,解答下列问题:
“读书好,读好书,好读书.”阅读对人成长的影响是巨大的,一本好书往往能改变人的一生.为了培养学生的读书习惯,某校组织学生开展“绿色大阅读”活动.右图是在活动之初某校对三个年级学生信息做的一个调查.图1是人数分布扇形统计图,其中八年级人数为408人,表2是该校学生阅读课外书籍情况统计表.请你根据图表中的信息,解答下列问题: