题目内容
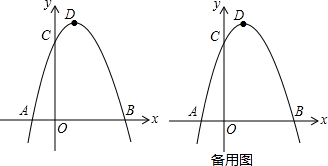
13.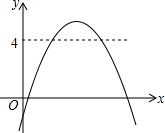 已知函数y=ax2+bx+c(a,b,c为常数.且a≠0)的图象如图所示,则关于x的方程ax2+bx+c-4=0的根的情况是( )
已知函数y=ax2+bx+c(a,b,c为常数.且a≠0)的图象如图所示,则关于x的方程ax2+bx+c-4=0的根的情况是( )| A. | 有两个不相等的正实数根 | B. | 有两个异号实数根 | ||
| C. | 有两个相等实数根 | D. | 无实数根 |
分析 根据抛物线的顶点坐标的纵坐标为大于4,判断方程ax2+bx+c-4=0的根的情况即是判断y=4时x的值,即可得出结果.
解答 解:∵y=ax2+bx+c(a,b,c为常数.且a≠0)的图象与x轴有两个交点,顶点坐标的纵坐标>4,
∵方程ax2+bx+c-4=0,
∴ax2+bx+c=4时,即是y=4求x的值,
由图象可知:有两个不相等的正实数根,
故选:A.
点评 此题主要考查了抛物线与x轴的交点、方程ax2+bx+c-4=0的根的情况;先看函数y=ax2+bx+c的图象的顶点坐标纵坐标,再通过图象可得到结果是解决问题的关键.

练习册系列答案
相关题目
 如图,点O为BC所在圆的圆心,∠BOC=128°,点D在BA的延长线上,AD=AC,则∠D=32°.
如图,点O为BC所在圆的圆心,∠BOC=128°,点D在BA的延长线上,AD=AC,则∠D=32°.