题目内容
18.如图,抛物线y=-x2+bx+c与x轴相交于A、B两点,与y轴相交于点C(0,3),点B坐标是(3,0),设抛物线的顶点为点D.(1)求此抛物线的解析式与对称轴;
(2)作直线BC,与抛物线的对称轴交于点E,点P为直线BC上方的二次函数上一个动点(且点P与点B、C不重合),过点P作PF∥DE交直线BC于点F,设点P的横坐标为m;
①用含m的代数式表示线段PF的长,并求出当m为何值时,四边形PDEF为平行四边形?
②设△PBC的面积为S,求S与m的函数关系式.S是否存在最大值?若存在,求出最大值并求出此时P点坐标,若不存在,说明理由.
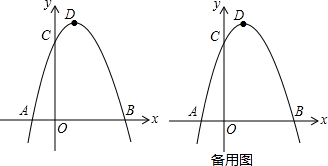
分析 (1)将点C(0,3)、B(3,0)代入抛物线的解析式可求得得:$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$,从而求得抛物线的解析式为y=-x2+2x+3,由x=-$\frac{b}{2a}$可求得抛物线的对称轴方程为x=1;
(2)①如图1所示:先求得点D的坐标,然后依据待定系数法求得直线BC的解析式为y=-x+3,将x=1代入y=-x+3得y=2,从而得到ED=2,由点P的横坐标为m,可求得yp=-m2+2m+3,yF=-m+3.故此PF=yp-yF=-m2+3m.当PF=DE=2时四边形PDEF为平行四边形,从而可求得m=2;
②由${S}_{△PCB}=\frac{1}{2}OB•PF$可知S=-$\frac{3}{2}(m-\frac{3}{2})^{2}$+$\frac{27}{8}$,故此可知当m=$\frac{3}{2}$时,最大值为$\frac{27}{8}$.将x=$\frac{3}{2}$代入抛物线的解析式得:y=$\frac{15}{4}$.故此可知点P的坐标为($\frac{3}{2}$,$\frac{15}{4}$).
解答 解:(1)将点C(0,3)、B(3,0)代入抛物线的解析式得:$\left\{\begin{array}{l}{-9+3b+c=0}\\{c=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$,
抛物线的解析式为y=-x2+2x+3.
∵x=-$\frac{b}{2a}$,
∴x=-$\frac{2}{-1×2}$=1.
∴抛物线的对称轴为x=1.
(2)①如图1所示:
∵将x=1代入得抛物线的解析式得y=4.
∴点D的坐标为(1,4).
设直线BC的解析式为ykx+b,将点B、C的坐标代入得:$\left\{\begin{array}{l}{3k+b=0}\\{b=3}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-1}\\{b=3}\end{array}\right.$.
∴直线BC的解析式为y=-x+3.
将x=1代入y=-x+3得:y=-1+3=2.
∴点E的坐标为(1,2).
∴DE=2.
∵点P的横坐标为m,
∴yp=-m2+2m+3,yF=-m+3.
∴PF=yp-yF=-m2+3m.
∵四边形PDEF为平行四边形,
∴PF=DE=2,即-m2+3m=2.
解得:m=2或m=1(舍去).
∴当m=2时,四边形PDEF为平行四边形.
②存在:
理由:如图2所示:
${S}_{△PCB}=\frac{1}{2}OB•PF$=$\frac{1}{2}×3×(-{m}^{2}+3m)$=-$\frac{3}{2}$(m2-3m)=-$\frac{3}{2}(m-\frac{3}{2})^{2}$+$\frac{27}{8}$.
当m=$\frac{3}{2}$时,△PBC的面积由最大值,最大值为$\frac{27}{8}$.
∵将x=$\frac{3}{2}$代入抛物线的解析式得:y=$\frac{15}{4}$.
∴点P的坐标为($\frac{3}{2}$,$\frac{15}{4}$).
点评 本题主要考查的二次函数的综合应用,解答本题需要同学熟练掌握二次函数和一次函数的性质、平行四边形的性质、三角形的面积公式、待定系数法求一次函数的解析式,明确PF的长等于点P与点F的纵坐标之差是解题的关键.

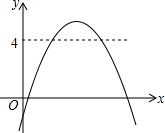 已知函数y=ax2+bx+c(a,b,c为常数.且a≠0)的图象如图所示,则关于x的方程ax2+bx+c-4=0的根的情况是( )
已知函数y=ax2+bx+c(a,b,c为常数.且a≠0)的图象如图所示,则关于x的方程ax2+bx+c-4=0的根的情况是( )| A. | 有两个不相等的正实数根 | B. | 有两个异号实数根 | ||
| C. | 有两个相等实数根 | D. | 无实数根 |
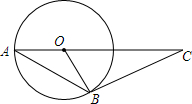 如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠ABO=25°,则∠C的度数是( )
如图,AB是⊙O的弦,AO的延长线交过点B的⊙O的切线于点C,如果∠ABO=25°,则∠C的度数是( )| A. | 65° | B. | 50° | C. | 40° | D. | 25° |
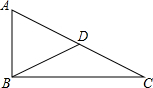 如图,Rt△ABC中∠ABC=90°,D为斜边AC的中点,AC=20cm,则BD=10cm.
如图,Rt△ABC中∠ABC=90°,D为斜边AC的中点,AC=20cm,则BD=10cm.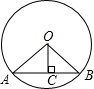 如图,AB是⊙O的弦,OC⊥AB,垂足为C,若OA=5,OC=4,则AB的长为6.
如图,AB是⊙O的弦,OC⊥AB,垂足为C,若OA=5,OC=4,则AB的长为6.
 一只蜘蛛正处于一个正方体的一个顶点A处,一只苍蝇处于此正方体的另一个顶点B处(如图所示),如果此正方体的棱长恰为10cm,试问蜘蛛想捉到苍蝇的最短路线是10$\sqrt{5}$cm.
一只蜘蛛正处于一个正方体的一个顶点A处,一只苍蝇处于此正方体的另一个顶点B处(如图所示),如果此正方体的棱长恰为10cm,试问蜘蛛想捉到苍蝇的最短路线是10$\sqrt{5}$cm.