题目内容
4. 如图,点O为BC所在圆的圆心,∠BOC=128°,点D在BA的延长线上,AD=AC,则∠D=32°.
如图,点O为BC所在圆的圆心,∠BOC=128°,点D在BA的延长线上,AD=AC,则∠D=32°.
分析 由AD=AC,可得∠ACD=∠ADC,由∠BAC=∠ACD+∠ADC=2∠D,可得∠BAC的度数,由∠D=$\frac{1}{2}$∠BAC即可求解.
解答 解:∵AD=AC,
∴∠ACD=∠ADC,
∵∠BAC=∠ACD+∠ADC=2∠D,
∴∠BAC=$\frac{1}{2}$∠BOC=$\frac{1}{2}$×128°=64°,
∴∠D=$\frac{1}{2}$∠BAC=32°.
故答案为:32°.
点评 本题主要考查了圆周角及等腰三角形的性质,解题的关键是找出∠D与∠BOC的关系.

练习册系列答案
相关题目
13.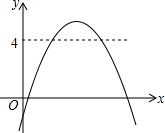 已知函数y=ax2+bx+c(a,b,c为常数.且a≠0)的图象如图所示,则关于x的方程ax2+bx+c-4=0的根的情况是( )
已知函数y=ax2+bx+c(a,b,c为常数.且a≠0)的图象如图所示,则关于x的方程ax2+bx+c-4=0的根的情况是( )
 已知函数y=ax2+bx+c(a,b,c为常数.且a≠0)的图象如图所示,则关于x的方程ax2+bx+c-4=0的根的情况是( )
已知函数y=ax2+bx+c(a,b,c为常数.且a≠0)的图象如图所示,则关于x的方程ax2+bx+c-4=0的根的情况是( )| A. | 有两个不相等的正实数根 | B. | 有两个异号实数根 | ||
| C. | 有两个相等实数根 | D. | 无实数根 |
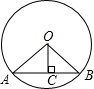 如图,AB是⊙O的弦,OC⊥AB,垂足为C,若OA=5,OC=4,则AB的长为6.
如图,AB是⊙O的弦,OC⊥AB,垂足为C,若OA=5,OC=4,则AB的长为6.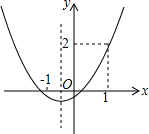 已知抛物线y=ax2+bx+c的图象如图所示,则下列结论:①abc>0;②a+b+c=2;③a<$\frac{1}{2}$;④b>1.其中正确的结论是②④.
已知抛物线y=ax2+bx+c的图象如图所示,则下列结论:①abc>0;②a+b+c=2;③a<$\frac{1}{2}$;④b>1.其中正确的结论是②④.