题目内容
10.三个连续的奇数,最大的一个是2n+1,将这三个连续的奇数按照从小到大顺序排列,得到一个三位数.(1)用整式表示这个三位数,并化简;
(2)当n为何值时,这个三位数的值最大值?并求出这个最大值.
分析 (1)由题意可知最小的数是2n-3,然后是2n-1,最后是2n+1,从而可以解答本题;
(2)根据题意可知最大的数是9,从而可以解答本题.
解答 解:(1)由题意可得,
100(2n-3)+10(2n-1)+(2n+1)
=200n-300+20n-10+2n+1
=222n-309,
即这个三位数是222n-309;
(2)由题意可得,
当2n+1=9时,得n=4,此时这个三位数的最大,此时这个三位数是579,
即当n=4时,这个三位数的最大,此时这个三位数是579.
点评 本题考查列代数式,解题的关键是明确题意,找出所求问题需要的条件.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
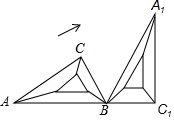 如图,将三角尺ABC(其中∠ABC=60°,∠C=90°)绕B点按顺时针转动一个角度到A1BCl的位置,使得点A,B,C1在同一条直线上,那么这个旋转角的度数等于120°.
如图,将三角尺ABC(其中∠ABC=60°,∠C=90°)绕B点按顺时针转动一个角度到A1BCl的位置,使得点A,B,C1在同一条直线上,那么这个旋转角的度数等于120°.