题目内容
5.把抛物线y=x2-6x向上平移k个单位,新的抛物线顶点坐标为M,与y轴交于点N,P(4,6),当△PMN的面积为20时,则k=$\frac{14}{3}$.分析 根据平移规律得到新抛物线解析式,易得N的坐标,求直线PN的解析式,表示出与抛物线对称轴的交点A的坐标,根据顶点M的坐标表示线段AM的长,由三角形的面积公式=铅直高度×水平距离,进行解答.
解答 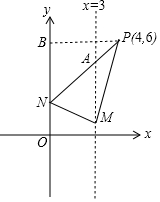 解:把抛物线y=x2-6x=(x-3)2-9向上平移k个单位,得到y=(x-3)2-9+k,
解:把抛物线y=x2-6x=(x-3)2-9向上平移k个单位,得到y=(x-3)2-9+k,
则顶点M(3,-9+k),N(0,k),
设PN的解析式为:y=ax+b,
把P(4,6)、N(0,k)代入得:$\left\{\begin{array}{l}{4a+b=6}\\{b=k}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=\frac{6-k}{4}}\\{b=k}\end{array}\right.$,
∴PN的解析式为:y=$\frac{6-k}{4}$x+k,
当x=3时,y=$\frac{3(6-k)}{4}$+k=$\frac{1}{4}$k+$\frac{9}{2}$,
∵抛物线的开口向上,
∴抛物线与y轴的交点N总在顶点M的上方,
∴AM=$\frac{1}{4}$k+$\frac{9}{2}$-(-9+k)=-$\frac{3}{4}$k+$\frac{27}{2}$,
过P作PB⊥y轴于B,
∵P(4,6),
∴PB=4,
∵△PMN的面积为20,
∴$\frac{1}{2}$AM•PB=20,
$\frac{1}{2}$(-$\frac{3}{4}$k+$\frac{27}{2}$)×4=20,
k=$\frac{14}{3}$;
故答案为:$\frac{14}{3}$.
点评 本题考查了二次函数的图象与几何变换,熟知二次函数图象的平移法则是解答此题的关键,明确上移→+,下移→-,左移→+,右移→-的原则;并注意不规则三角形面积的求法:三角形的面积公式=铅直高度×水平距离,这在函数的问题中经常运用,要熟练掌握.

| A. | 3 | B. | 4 | C. | 0 | D. | 7 |
| A. | -1007 | B. | -1008 | C. | -1009 | D. | -2016 |
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 无实数根 | D. | 无法确定 |
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
| A. | (x+4)2=17 | B. | (x-4)2=17 | C. | (x+4)2=15 | D. | (x-4)2=15 |